MATLAB

MEX functions

Nota: Esta guía se hizo basada en una distribucion Linux. Los ejemplos y la estructura de directorios referenciada puede variar de un Sistema Operativo a otro.

Un archivo MEX es un archivo que permite llamar una función escrita en C desde Matlab (es una abreviación de 'MATLAB executable'). Para ello se hace uso del comando de Matlab mex y de un compilador compatible instalado en el sistema operativo.

Eligiendo compilador

Para el sistema operativo Linux la version por defecto del compilador es GCC versión ‘6.3.X’. La lista de compiladores compatibles de acuerdo al sistema instalado se puede consultar aquí. Para corroborar que su sistema posee un compilador compatible (o elegir entre más de un compilador, si su sistema los posee) ejecute lo siguiente:

   >> mex -setup
   MEX configured to use 'gcc' for C language compilation.

Un primer programa ‘Hola mundo’

El objetivo de esta seccion es compilar y ejecutar el contenido de un archivo C sencillo desde Matlab.
Pasos:

1. Utilizando su editor de texto favorito, cree un archivo llamado ‘hola.c’ en su área de trabajo de Matlab. Su área de trabajo actual la puede encontrar ejecutando

   >> pwd

2. Agregue el siguiente contenido a su archivo ‘hola.c’

   #include "mex.h"
   
   void mexFunction(int nlhs,mxArray *plhs[],int nrhs,const mxArray *prhs[]){
      printf("Hola mundo!\n");
      return;
   }

Note que el header mex.h es requerido en el archivo. Éste contiene las funciones del API de Matlab. Las demás secciones seran explicadas a lo largo de esta guía.

3.Una vez guardado el archivo, desde la consola de Matlab ejecute

   >> mex hola.c
   Building with 'gcc'.
   MEX completed successfully.

4. Una vez que el archivo ha sido satisfactoriamente compilado la función MEX ‘hola’ estará disponible para usarse desde la consola de Matlab:

   >> hola
   Hola mundo!

Utilizando una función C existente para crear un archivo MEX

Suponga que se tiene el siguiente código funcional en C:

#include<stdio.h>

void arrayProduct(double x, double *y, double *z, int n);

void main(){
   double vect0[] = {3,2,5,4};
   double cval = 4;
   double vect1[4];
   arrayProduct(cval, vect0, vect1, 4);
   printf("Third scaled value is %3.2f\n", vect1[2]);
}

void arrayProduct(double x, double *y, double *z, int n){
  int i;
  
  for (i=0; i<n; i++) {
    z[i] = x * y[i];
  }
}

el cual simplemente escala un vector dado por una constante, usando para ello la función arrayProduct. Se requiere crear un archivo MEX de manera que la funcionalidad de arrayProduct se pueda usar directamente desde Matlab, por ejemplo:

>>s = 5; 
>>A = [1.5, 2, 9];
>>B = arrayProduct(s,A)
B =
    7.5000   10.0000   45.0000 

Creando el archivo fuente: La función mexFunction

En esta sección se creará el archivo fuente para ser usado por Matlab. Cree un archivo *.c y agregue el siguiente header para poder usar el API de Matlab (en este ejemplo, es nombrado como cvector.c)

#include "mex.h"

Lo siguiente es agregar la función mexFunction. Esta función es requerida en cualquier archivo *.c que se desee compilar con mex, y es el puente entre nuestro código C y Matlab. Cada vez que una función MEX es llamada Matlab busca en el código correspondiente a la función mexFunction. Si mexFunction no es encontrada entonces un error es disparado. La función mexFunction tiene la siguiente firma:

void mexFunction(int nlhs, mxArray *plhs[],
                 int nrhs, const mxArray *prhs[])

Los argumentos se detallan en la siguiente tabla.

Tabla 1. Argumentos de la MEX function.

nlhs	Número de argumentos de salida, o bien el tamaño del arreglo plhs
plhs	Arreglo de punteros a los argumentos de salida.
nrhs	Número de argumentos de entrada, o bien el tamaño del arreglo prhs
prhs	Arreglo de punteros a los argumentos de entrada.

Note que los argumentos de entrada o salida son del tipo mxArray, el cual es el tipo del 'arreglo de Matlab' (En Matlab todas las variables (escalares, vectores, matrices, objetos …) son guardadas como arreglos. Al declararse una variable de Matlab en C este tipo de variable debe de ser explícito).

En nuestro caso, queremos definir un arreglo de tamaño arbitrario en Matlab y definir una constante para multiplicar cada entrada de este arreglo. Buscamos algo como

>> s = 5;
>> A = [3,2,8];
>> B = cvector(s,A);

Entonces estaremos enviando por medio del argumento prhs la constante en la primera posición (s en el código anterior), y el vector en la segunda posición (A en el código anterior).

Recibiendo los datos en la función mexFunction y preparando la salida

Necesitamos entonces saber interpretar nuestro arreglo de entrada y preparar la salida de forma consistente con lo que se quiere hacer (funcion cvector en nuestro caso). El código que debemos agregar nuestra función mexFunction se presenta a continuación.

void mexFunction( int nlhs, mxArray *plhs[],
                  int nrhs, const mxArray *prhs[]){

   double multiplier;      /* input scalar */
   double *inMatrix;       /* 1xN input matrix */                     
   
   mwSize ncols;           /* size of matrix */
   double *outMatrix;      /* output matrix */
   
   multiplier = mxGetScalar(prhs[0]);
   inMatrix = mxGetDoubles(prhs[1]);
   
   ncols = mxGetN(prhs[1]);

   /* create the output matrix */
   
   plhs[0] = mxCreateDoubleMatrix(1,ncols,mxREAL);

   /* get a pointer to the real data in the output matrix */
   outMatrix = mxGetDoubles(plhs[0]);
   
   /* call the computational routine */
   arrayProduct(multiplier,inMatrix,outMatrix,ncols);

}

En la variable multiplier guardaremos el escalar de entrada, que como sabemos de las especificaciones está dada en la primera posición del arreglo de entrada. Usamos la función de Matlab mxGetScalar que devuelve la parte real del primer elemento de un arreglo del tipo mxArray. Seguidamente recibimos el vector usando la función mxGetDoubles que devuelve los elementos reales de un arreglo, y la guardamos en inMatrix. Mas detalles sobre estas funciones pueden ser consultados acá.

El número de columnas es guardado en ncols. Note que esta variable es del tipo mwSize. El tipo mwSize es una macro que permite redefinir el tamaño del entero basado en la plataforma que se esté trabajando, lo cual brinda flexibilidad. Para ser consistente, la definción de i en la función arrayProduct será redefinido posteriormente al tipo mwSize también.

La cantidad de columnas del arreglo es guardada en ncols por medio de la función mxGetN que devuelve la cantidad de columnas de un arreglo.

Seguidamente se prepara la salida de nuestra función. Creamos primero el arreglo de salida plhs de una fila, n columnas y de tipo real. Las entradas reales de este arreglo las guardamos a continuación en outMatrix.

Nuestra función mexFunction está lista ahora para recibir las variables desde Matlab y devolver la salida.

Agregando nuestra función C

Finalmente, agregamos nuestra función C al archivo que vamos a compilar con mex.

#include "mex.h"

void arrayProduct(double x, double *y, double *z, mwSize n){
  mwSize i;
  
  for (i=0; i<n; i++) {
    z[i] = x * y[i];
  }
}

void mexFunction( int nlhs, mxArray *plhs[],
(…)

Note que la variable i se redifinió a mwSize, como se había anticipado.

Compilando nuestro archivo C con mex

Con nuestro archivo cvector.c listo procedemos a compilar con mex (La opción -R2018a es requerida porque en este ejemplo se han usado funciones del más reciente API de Matlab. Más específicamente, esta opción se usa para hacer uso del interleaved complex API )

>> mex cvector.c -R2018a
Building with 'gcc'.
MEX completed successfully.

En seguida, procedemos a crear un vector de ejemplo y una constante arbitraria para usar nuestra función MEX.

>> c = 3
c =
     3
>> A = [2,5,6,3.5]
A =
    2.0000    5.0000    6.0000    3.5000
>> cvector(c,A)
ans =
    6.0000   15.0000   18.0000   10.5000

Arreglos de tamaño variable

Nótese que en el ejemplo anterior el tamaño del arreglo de entrada nunca se definió a algún valor fijo. Retomemos el código de nuestra mexFunction:

   (...)
   double *inMatrix;       /* 1xN input matrix */                     
   
   mwSize ncols;           /* size of matrix */
   double *outMatrix;      /* output matrix */
   
   multiplier = mxGetScalar(prhs[0]);
   inMatrix = mxGetDoubles(prhs[1]);
   
   ncols = mxGetN(prhs[1]);
   (...)

Note que para recibir el vector de entrada se utiliza el puntero inMatrix. El vector de entrada recordemos que corresponde a la posición 1 del arreglo de punteros de entrada prhs, el cual es de tamaño arbitrario. Posteriormente el tamaño de este arreglo de entrada se obtiene con mxGetN el cual servirá luego como parámetro en nuestra función de C que multiplica el vector por el escalar.

En el ejemplo se utilizó un vector de entrada de 3 valores pero perfectamente se puede cambiar. Por ejemplo,

>> c = 2;
>> B = [1,2,3,4,5,6,7,8,9];
>> cvector(c,B)

ans =

     2     4     6     8    10    12    14    16    18

Validando entradas y salidas y añadiendo mensajes

Una vez que nuestro código es funcional, podemos proceder a hacerlo más robusto agregando mensajes o bien validando el tipo y la cantidad de los argumentos de entrada y salida. Para asegurar que la entrada conste de 2 argumentos y la salida de 1 argumento añadimos el siguiente código en nuestra mexFunction:

if(nrhs != 2) {
    mexErrMsgIdAndTxt("MyToolbox:cvector:nrhs",”Dos entradas requeridas");
}
if(nlhs != 1) {
    mexErrMsgIdAndTxt("MyToolbox:cvector:nlhs","Una salida requerida");
}

El siguiente código valida que el primer argumento sea un escalar del tipo double.

/* make sure the first input argument is scalar */
if( !mxIsDouble(prhs[0]) || mxGetNumberOfElements(prhs[0]) != 1 ) {
    mexErrMsgIdAndTxt("MyToolbox:cvector:notScalar",
                      "Entrada debe ser un escalar");
}

En el código anterior se ha usado la función mxIsDouble que revisa si la entrada es del tipo double y además la función mxGetNumberOfElements que devuelve la cantidad de elementos de un array. Recuerde que prhs[0] contiene el escalar por el que queremos multiplicar el vector.

Similarmente, podemos revisar si el segundo argumento de entrada corresponde a un vector fila:

/* check that number of rows in second input argument is 1 */
if(mxGetM(prhs[1]) != 1) {
    mexErrMsgIdAndTxt("MyToolbox:cvector:notRowVector", "Entrada no es un vector fila");
}

En este caso se usó la función mxGetM la cual devuelve la cantidad de filas en un arreglo.

En el código anterior se ha usado la función mexErrMsgIdAndTxt, en la cual además se incluyó un “identificador de mensaje” el cual usa la sintáxis

 
componente:mnemotécnico

Para evitar el uso de un identificar de mensaje se puede usar la versión simplificada mexErrMsgTxt

mexErrMsgTxt("Entrada debe ser un escalar");

La función mexPrintf imprime mensajes a como lo hace printf en C. También se dispone de la función mexWarnMsgIdAndTxt para imprimir warnings. Este último permite notificar errores o advertencias sin terminar la función MEX.

Pidiendo un número al usuario

Otra de las funcionalidades básicas que puede ser deseable añadir a nuestra función es pedir un número al usuario. Las funciones de C scanf y printf no son compatibles con Matlab. En lugar, usaremos la función input de Matlab en nuestra función MEX

>> input('Digite un número')
Digite un número5

ans =

     5

El siguiente código muestra cómo podemos pedir un número al usuario desde nuestra función MEX:

#include "mex.h"
#include "string.h"
void mexFunction( int nlhs, mxArray *plhs[],
                  int nrhs, const mxArray *prhs[] ){
  mxArray   *new_number, *str;
  double out;

  str = mxCreateString("Ingrese un número");
  mexCallMATLAB(1,&new_number,1,&str,"input");
  out = mxGetScalar(new_number);
  mexPrintf("El número ingresado es: %.0f ", out);
  mxDestroyArray(new_number);
  mxDestroyArray(str);
  return;
}

Aquí hacemos uso de la función mexCallMATLAB que está definida como

int mexCallMATLAB(int nlhs, mxArray *plhs[], int nrhs,
  mxArray *prhs[], const char *functionName);

donde los argumentos son análogos a los de la tabla 1. En nuestro caso, tenemos 1 argumento de salida (new_number) y 1 argumento de entrada (el texto con el mensaje que ve el usuario). Por medio de mxDestroyArray liberamos la memoria dinámica utilizada en los argumentos de entrada (NO debe usarse en los argumentos de salida).

Level-2 S-Functions

Una S-Function es una descripción por medio de código de un bloque de Simulink. Estas funciones se pueden escribir en lenguaje Matlab, C, C++ o Fortran. Esta guía se enfocará en el lenguaje C. Las funciones nivel 2 o Level-2 S-Functions fueron introducidas con la versión de Simulink 2.2. La versión anterior, Level-1 S-Functions, escritas para trabajar con Simulink versión 2.1 y anteriores son compatibles con la versión 2.2. Sin embargo para hacer uso de todas las nuevas características se recomienda escribir Level-2 S-Functions.

Corriendo un ejemplo

En esta sección se ejemplificará cómo usar el programa en C llamado timestwo.c de Matlab en Simulink.

El primer paso es copiar el archivo timestwo.c a su área de trabajo. Ejecute el siguiente comando para copiar el archivo:

>> copyfile(fullfile(matlabroot,'toolbox','simulink','simdemos','simfeatures','src','timestwo.c'),'.')

Una vez que el archivo esté en su área de trabajo, proceda a compilarlo usando el comando mex

>> mex timestwo.c
Building with 'gcc'.
MEX completed successfully.

Inicialice Simulink. Una forma de hacerlo es por medio del símbolo de la siguiente figura, el cual puede localizarse en la barra superior de tareas de Matlab.

Figura 1. Icono de Simulink

Una vez con Simulink ejecutándose, elija por comodidad el modelo “Simulación simple”, en la pestaña de “Nuevo”, como se ve en la siguiente figura.

Figura 2. Eligiendo un nuevo modelo en Simulink

El objetivo será usar un diagrama de bloques similar al de la figura 3, por lo que proceda a borrar los componentes a excepción del generador de la onda de seno y el scope.

Figura 3. Diagrama de bloques por construir.

Seguidamente vaya a 'Herramientas > Buscador de librerías'. En la nueva ventana de opciones, bajo la categoría de Simulink busque la opción de “Funciones definidas por el usuario” y arrastre el bloque de código C. Ver figura 4.

Figura 4. Eligiendo funciones definidas por el usuario

Dando click derecho en el nuevo bloque, elija la opción de “Parámetros de bloque (S-Function)”. Ingrese el nombre de la función en el campo correspondiente y deje los demás campos intactos. Refiérase a la figura 5.

Figura 5. Opciones para la S-Function

Revise qué amplitud tiene la onda de seno del generador (dando doble click sobre el bloque) y proceda a correr la simulación por medio de 'Simulación>Correr'. Observe en el scope (dando doble click sobre su bloque) cómo la amplitud de la función de seno ha sido duplicada.

Explicación del ejemplo

El ejemplo de la sección anterior se compone de 3 partes principales:

• Definiciones y librerías por importar.
• Callback methods.
• Interfaces del producto Simulink o Simulink Coder.

Definiciones y librerías

Las definiciones indican el nombre de la S-Function y el tipo de nivel (1 o 2).

#define S_FUNCTION_NAME timestwo 
#define S_FUNCTION_LEVEL 2

Seguidamente se importa el header simstruc.h, el cual nos permite hacer uso de la estructura SimStruct.

#include "simstruc.h"

Esta estructura permite a Simulink guardar u obtener información sobre nuestra S-Function. Este header permite también encapsular la información relacionada con la S-Function, como los parámetros y salidas, para hacer posible el acceso con la estructura SimStruct.

Callback methods

La ejecución de un modelo de Simulink conlleva diferentes etapas. La primer etapa es la inicialización, en la cual Simulink propaga el tamaño de las señales, tipos de datos, tiempos de muestreo, orden de ejecución de bloques y alojamiento de memoria. Seguidamente procede un bucle o ciclo donde se ejecutan los bloques del modelo (en el orden fijado durante la inicialización) y se calculan las salidas. El diagrama de la figura 6 muestra este proceso.

Figura 6. Etapas de la simulación.

Los callback methods ejecutan las tareas requeridas en cada etapa de la simulación. La descripción de éstos en nuestro ejemplo se detallan a continuación.

a) mdlInitializeSizes

Es llamado por Simulink para obtener la cantidad de puertos de entrada y salida, tamaños de puertos y cualquier otra información relevante (como el número de etapas).

En nuestro caso tenemos especificado mediante este código que la cantidad de parámetros es cero:

    ssSetNumSFcnParams(S, 0);
    if (ssGetNumSFcnParams(S) != ssGetSFcnParamsCount(S)) {
        return; /* Parameter mismatch will be reported by Simulink */
    }

Esta es la razón por la que se dejó en blanco la información de parámetros en la figura 5. Además del código se observa que un error es disparado si la cantidad de parámetros especificada por el usuario no es consistente con lo esperado.

Mediante el siguiente código especificamos que la cantidad de puertos es 1 de entrada y 1 de salida:

    if (!ssSetNumInputPorts(S, 1)) return;
    ssSetInputPortWidth(S, 0, DYNAMICALLY_SIZED);
    ssSetInputPortDirectFeedThrough(S, 0, 1);

    if (!ssSetNumOutputPorts(S,1)) return;
    ssSetOutputPortWidth(S, 0, DYNAMICALLY_SIZED);

Además el tamaño de estos puertos es definido dinámicamente. Esto hace que nuestro bloque acepte señales de cualquier tamaño. La declaración ssSetInputPortDirectFeedThrough indica el feedthrough del puerto. Si no se especifica el valor por defecto 0, lo cual es equivalente a indicar que el puerto no se usa en mdlOutputs (ver sección c) abajo).

El número de tiempos de muestreo se especifican con este código (ver sección b) abajo):

    ssSetNumSampleTimes(S, 1);

Otras opciones adicionales pueden ser agregadas. Por ejemplo, la opción de exception free code puede ser añadida para aumentar la velocidad de ejecución de la S-Function, pero no debe de ser usada cuando nuestra función interactúe con el ambiente de Matlab.

    ssSetOptions(S,
                 SS_OPTION_WORKS_WITH_CODE_REUSE |
                 SS_OPTION_EXCEPTION_FREE_CODE |
                 SS_OPTION_USE_TLC_WITH_ACCELERATOR);

b) mdlInitializeSampleTimes

Es llamado por Simulink para configurar los tiempos de muestreo de la S-Function. Estos tiempos pueden depender de si el modelo corre en específicos rates o si por ejemplo corre cuando es disparado por otro bloque. En nuestro ejemplo, nuestra función corre simplemente cuando la señal de entrada se presente, por lo que usa un tiempo de muestreo “heredado”, INHERITED_SAMPLE_TIME.

c) mdlOutputs

Este callback method es llamado para calcular la salida del bloque. Para recordar, nuestro ejemplo multiplica la señal de entrada por 2 y escribe este resultado en la salida. El código usado se muestra a continuación.

static void mdlOutputs(SimStruct *S, int_T tid){
    int_T             i;
    InputRealPtrsType uPtrs = ssGetInputPortRealSignalPtrs(S,0);
    real_T            *y    = ssGetOutputPortRealSignal(S,0);
    int_T             width = ssGetOutputPortWidth(S,0);

    for (i=0; i<width; i++) {
        *y++ = 2.0 *(*uPtrs[i]); 
    }
}

La señal de entrada es accesada por medio de la macro ssGetInputPortRealSignalPtrs. Esta macro devuelve un vector de punteros que deben ser accesados por

*uPtrs[i]

Similarmente, los puertos de salida con accesados por medio de la macro ssGetOutputPortRealSignal. El ancho de las señales de obtiene con ssGetOutputPortWidth. A continuación simplemente se itera la entrada para calcular la salida.

d) mdlTerminate

Es usado para ejecutar tareas después de la simulación. En nuestro ejemplo ninguna tarea se ejecuta, pero la declaración de la rutina es obligatoria.

static void mdlTerminate(SimStruct *S){
}

Interfaces del producto Simulink o Simulink Coder

Esta porción de código debe ser incluida al final de nuestro archivo:

#ifdef  MATLAB_MEX_FILE    /* Is this file being compiled as a MEX-file? */
#include "simulink.c"      /* MEX-file interface mechanism */
#else
#include "cg_sfun.h"       /* Code generation registration function */
#endif

Esto selecciona el código correcto dependiendo de cómo compilamos el archivo (en esta guía solo hemos compilado con el comando mex).

Usando un template para escribir la S-Function

Para facilitar la escritura de una S-Function se puede hacer uso de un template localizado en

matlabroot/simulink/src/sfuntmpl_basic.c

Todas las rutinas disponibles pueden ser consultadas en el archivo sfuntmpl_doc.c en el mismo directorio.

También, al importar el simstruct.h se importa una serie de librerías necesarias. Una de ellas contiene el tipo de datos que se pueden usar en la S-Function. Esta librería es

matlabroot/extern/include/tmwtypes.h

Como se observó, se hizo uso de tipos como “real_T” o “int_T”. Sin embargo estos tipos pueden cambiarse a los más familiares double e int y los resultados son idénticos.

Pasando parámetros a la S-Function

En esta sección se verá cómo pasar parámetros a una S-Function al inicio de la simulación, usando el campo correspondiente en el cuadro de diálogo de la figura 8. Simulink guarda los valores de estos parámetros en la SimStruct (ver sección 2.1.1.1). Por medio de los callback methods o macros de la SimStruct estos parámetros pueden usarse en nuestra función para calcular la salida. Durante este ejemplo se usará como base el archivo

matlabroot/toolbox/simulink/simdemos/simfeatures/src/sfun_runtime1.c

Los pasos para satisfactoriamente usar parámetros en nuestra S-Function son:

1) Determinar el orden en el que los parámetros deben ser especificados en el cuadro de diálogo.

2) Durante la función mdlInitializeSizes, usar la macro ssSetNumSFcnParams para indicar cuántos parámetros la S-Function acepta:

   static void mdlInitializeSizes(SimStruct *S){
      ssSetNumSFcnParams(S, NPARAMS);  /* Number of expected parameters */

El primer parámetro “S” corresponde a la instancia de la SimStruct y el segundo indica la cantidad de parámetros a usar. En este caso se usa el define NPARAMS el cual está fijado a 3.

3) Usar la macro ssGetSFcnParam para accesar los parámetros el cuadro de diálogo en la S-Function. Esta macro recibe 2 entradas: la instancia de la SimStruct y el índice del parámetro, siendo 0 el primer parámetro, 1 el segundo, etc. En este caso los 3 parámetros y su orden son:

   #define SIGNS_IDX 0
   #define SIGNS_PARAM(S) ssGetSFcnParam(S,SIGNS_IDX)

   #define GAIN_IDX  1
   #define GAIN_PARAM(S) ssGetSFcnParam(S,GAIN_IDX)

   #define OUT_IDX   2
   #define OUT_PARAM(S) ssGetSFcnParam(S,OUT_IDX)

Note que de antemano los parámetros son definidos también para usar la instancia “S” de la SimStruct.

Con estos pasos, los parámetros estarán listos para usarse en la S-Function, usando las funciones del API de Matlab mxGetNumberOfElements, mxGetString, etc, como se verá a continuación.

Corriendo el ejemplo

Siga los siguientes pasos:

1) Copie el archivo matlabroot/toolbox/simulink/simdemos/simfeatures/src/sfun_runtime1.c a su área de trabajo. Recuerde que una forma de copiar el archivo es por medio del siguiente comando desde Matlab

   copyfile(fullfile(matlabroot,'toolbox','simulink','simdemos','simfeatures','src','sfun_runtime1.c'),'.')

2) Compile el archivo con el comando mex.

3) Defina en su ambiente de Matlab una variable llamada gainVal y asigne el valor de 5 a esta variable:

   >> gainVal = 5;

4) Abra un nuevo proyecto en blanco de Simulink.

5) Desde 'Herramientas > Buscador' de librerías ingrese los siguientes componentes:

a) Un generador de onda de seno. Puede dejar sus valores por defecto (amplitud = 1)

b) Un bloque constante. Asigne el valor de 3 a este bloque.

c) Un scope.

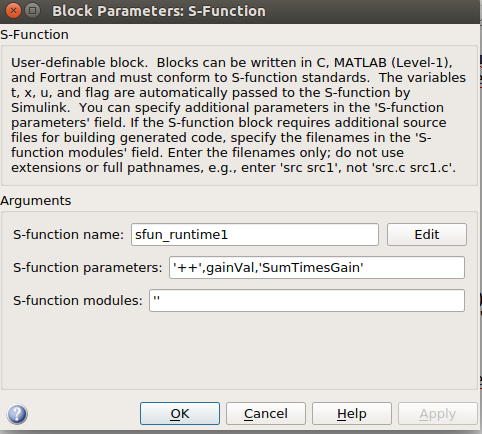
d) Un bloque de S-Function. En los “parámetros del bloque” (dando clic derecho, por ejemplo) indique el nombre de la S-Function y añada los parámetros '++', gainVal, 'SumTimesGain' separados por coma. La configuración se muestra en la siguiente figura.

Figura 7. Parámetros del ejemplo sfun_runtime1.c

e) Conecte la señal de seno y el bloque constante a la entrada de la S-Function y la salida de ésta al scope. La configuración se muestra en la siguiente figura.

Figura 8. Bloques del ejemplo.

6) Corra la simulación y observe su salida en el scope. El resultado debería lucir como en la figura siguiente.

Figura 9. Salida del scope.

¿Cómo funciona? Recordemos de la sección anterior que la función recibe 3 parámetros. El primer parámetro contiene la cantidad de puertos de entrada (en este ejemplo, una cantidad arbitraria pero mayor a 2) indicada por signos “++-” (los signos indican si las señales se suman o se restan). El segundo parámetro especifica una ganancia que se aplica a la suma de las señales de entrada. El tercer parámetro es alguno de los valores ‘SumTimesGain’ o ‘SumTimesGainAndAverage’ (ver también encabezado del archivo sfun_runtime.c). La salida consiste en el producto {suma de señales de entrada}x{ganancia}, en el caso de que ‘SumTimesGain’ sea especificado o bien {suma de señales de entrada}x{ganancia} y promedio de señales de entrada si ‘SumTimesGainAndAverage’ es especificado.

Note por ejemplo cómo las señales de entrada son asignadas de forma paramétrica (son una cantidad arbitraria). Durante la etapa de mdlInitializeSizes se tiene el siguiente código:

    {
        int_T nu = (int_T)mxGetNumberOfElements(SIGNS_PARAM(S));
        int_T i;

        if (!ssSetNumInputPorts(S, nu)) return;
        for (i = 0; i < nu; i++) {
            ssSetInputPortWidth(S, i, DYNAMICALLY_SIZED);
            ssSetInputPortDirectFeedThrough(S, i, 1);
            ssSetInputPortOverWritable(S, i, 1);
            ssSetInputPortOptimOpts(S, i, SS_REUSABLE_AND_LOCAL);
        }
    }

La cantidad de elementos guardados en el parámetro “SIGNS_PARAMS” (que contiene las señales ‘++’) se accede por medio de una función conocida del API de Matlab mxGetNumberOfElements. Luego se usa la función ssSetNumInputPorts que sirve para indicarle a la SimStruct de la función cuántos puertos de entrada tiene la función y seguidamente se configura iterativamente cada entrada (usando funciones conocidas según la sección 2.1.1.2 )

En el caso de la ganancia (segundo parámetro) en este ejemplo el parámetro se configura como ajustable (o tunable) para poder ser cambiado durante la simulación. Este código configura dicha funcionalidad:

    ssSetSFcnParamTunable(S,GAIN_IDX,true);
    ssSetSFcnParamTunable(S,SIGNS_IDX,false);
    ssSetSFcnParamTunable(S,OUT_IDX,false);  

Más aún, el ejemplo configura todos los puertos tunables como run time parameters, lo cual permite alterar cambiar los parámetros sin detener la simulación. Para más información, consulte la ayuda de la función ssUpdateAllTunableParamsAsRunTimeParams.

Parallel Computing Toolbox

El toolbox de cálculo paralelo o Parallel Computing Toolbox permite resolver problemas computacionales demandantes usando todo el potencial de procesadores multinúcleo, unidades GPU y clusters de computadoras. Mediante herramientas de alto nivel, este toolbox permite paralelizar aplicaciones de Matlab sin necesidar de usar programación CUDA (Compute Unified Device Architecture, de nVidia) o MPI (Message Passing Interface).

Configurando un parallel pool

Para la ejecución de tareas en paralelo es necesario configurar un parallel pool, indicando para ello la cantidad de workers que serán usados (el cuál evidentemente dependerá de las características del procesador). El comando a utilizar es parpool con la sintáxis

parpool(poolsize)

El valor por defecto del poolsize puede ser consultado en la sección de Environment y luego Parallel Preferences, o bien en la esquina inferior izquierda de la ventana de Matlab. La ventana de configuración es similar a la de la siguiente figura.

Figura 10. Configuración del pool.

El comando parfor

El comando parfor se usa para ejecutar un for utilzando los workers del parallel pool. La sintáxis es

parfor loopVar = initVal:endVal; statements; end

Así, en un código Matlab cuyo tiempo de ejecución se quiera optimizar una forma es simplemente cambiar los for por parfor. En la siguiente sección se verá un ejemplo.

Corriendo un ejemplo simple

En esa sección se usará un parfor cuyo contenido involucra una función MEX. Por comodidad se usará la función MEX cvector() definida anteriormente .

1. Cree un archivo *.m y defina un escalar arbitrario c y un vector arbitrario A.

2. Asegúrese de tener compilada la función cvector en aŕea de trabajo.

3. Configure el parallel pool con 4 workers.

4. Con el uso de un parfor iteradamente calcule

$\sum _{i=0}^{10}{c}^{i}A$

usando para esto la función cvector() y despliegue el resultado.

5. Para mostar el tiempo de ejecución utilice las instrucciones de Matlab tic y toc. Éstas deben ser colocadas antes y después del código al cual se quiere medir el tiempo, de la forma siguiente:

tic;
<statements>
toc;

6. Cada llamado al parpool abre una nueva sesión. Como nuestro archivo .m está siendo llamado desde una sesión interactiva de Matlab la sesión del parallel pool debe ser eliminada. Añada estas instrucciones al final de su archivo.

poolobj = gcp('nocreate');
delete(poolobj);

7. Corra la simulación y observe el tiempo de ejecución.

Una posible solución a este problema se presenta a continuación.

c = 2; % escalar arbitrario
A = [1,2,3]; % vector arbitrario
B = A;
parpool(4); % inicializacion del parallel pool
tic;
parfor x = 1:10
   S = cvector(c.^x,A); % llamado a la MEX function
   B = B+S;
end
toc;
disp(B);
poolobj = gcp('nocreate');
delete(poolobj);

Es importante notar que a diferencia de un for ordinario, Matlab limpia en cada interación el valor de cualquier variable temporal declarada en el parfor. Además, el uso de variables de reducción (variables que acumulan valor en cada iteración) es ilegal dentro de un parfor. Por ejemplo, si en el código anterior se usa algo como

   ...
   A = cvector(c,A);
   ...

un error es disparado. Ver más en Temporary Variables Intended as Reduction Variables

Mejorando el tiempo de compilación con mex

Se puede hacer uso también del Parallel Computing Toolbox para mejorar los tiempos de compilación con mex. Par ello se puede usar la función parfeval, la cual tiene la siguiente firma.

parfeval(p,fcn,numout,in1,in2,...)

donde p es la instancia del parallel pool actual, fcn es la función a ejecutar, numout es la cantidad de argumentos de salida esperados y in1, in2, ... son los argumentos de entrada.
Para compilar nuestro archivo cvector.c se puede usar el siguiente código de Matlab.

parpool(4); % inicializa el parallel pool
p = gcp(); % devuelve el actual parallel pool

parfeval(p, @mex, 0, '-R2018a', 'cvector.c')

% teminando la sesion
poolobj = gcp('nocreate');
delete(poolobj);

Problemas comunes

Versión de gcc

Matlab soporta la versión 6.3 de gcc. Para manejar diferentes versiones de gcc una opción es usar update-alternatives o bien manualmente indicar a Matlab dónde encontrarlo. Por ejemplo:

mex -R2018a GCC='/home/ubuntu/Downloads/gcc6.3/gcc-6.3.0/bin/gcc' cvector.c

Error: undefined reference to `mxGetDoubles'

En varias secciones de esta guía se usó la función mxGetDoubles y otras similares. Como se mencionó en la sección 1.3.4 esta familia de funciones corresponde al interleaved complex API y por lo tanto el llamado al comando mex debe acompañarse de -R2018a.

mex -R2018a filename.c