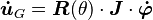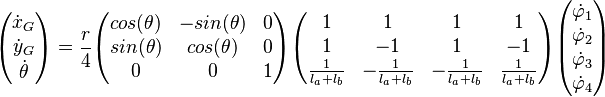MecanumRob

Tareas pendientes

• Instalar rejillas (cuando lleguen).
• Calibración de la IMU en la página del fabricante.
• Filtro para la IMU y obtención de postura(comparar con el filtro Madgwick que viene por defecto con el nodo).
• Botón para cambiar la velocidad máxima (análogo).
• Buscar algoritmos de evasión ya implementados en ROS.
• Calibración de evasión de obstáculos y comparativa de algoritmos.
• Documentación: arquitectura del software (diagramas y ejemplos de código, información de parámetros relevantes y launchfiles).
• Licencias para abrir el código y Copyright y sin garantía ("as is").
• Calibración de la odometría: sistema de adquisición de postura global basado en visión por computador.
• Obtener las covarianzas de los sensores: buscar los de la IMU en la página del fabricante.
• Calibración de SLAM.
• Fusión de los 2 sensores Hokuyo para el SLAM.
• Filtro de Kalman: implementación y filtrar mensajes por frecuencia más o menos constante.
• Deadman switch para ejecutar cualquier algoritmo si se presiona un botón.
• Buscar otros algoritmos SLAM.
• Propagar el software a los otros robots.
• Separar los puntos de anclaje para el transporte del robot.
• Migrar código de la base a C++.

Sensores y actuadores

• PhidgetsSpacial Precision 3/3/3 High Resolution [1]
• Roboclaw 2x30A Motor Controller (x2) [2]
• URG-04LX-UG01 Scanning Laser Rangefinder (x2) [3]

Calibración

IMU

Para la calibración del magnetómetro es necesario seguir las instrucciones de instalación de la librería phidgets para Ubuntu 16.04 y luego descargar y compilar el programa de calibración dado por el fabricante. En el comprimido se incluye un README con instrucciones. Para más información ver [4] y .

ROS

El MecanumRob usa los siguientes paquetes de ROS:

• mecanumrob_common: contiene las definiciones de menajes y servicios usados en los demás nodos, además de los .launch files, las reglas udev y el nodo para el control de play.
• mecanumrob_roboclaw: el controlador de las motores, envía los comandos a los motores y publica la velocidad de las ruedas.
• mecanumrob_model: el modelo cinemático del robot, tanto directo como inverso. Además el nodo que publica las transformaciones (próximamente el filtro de Kalman) y las pruebas para la odometría.
• vfhp_local_planner: el módulo de evasión de obstáculos.
• urg_node: controla un sensor Hokuyo.
• phidgets_imu: controla la IMU.
• gmapping: SLAM basado en las lecturas de los sensores láser.

Servicio

Para hacer que ROS corra automáticamente desde el arranque se usó el paquete robot_upstart. Lo que hace este paquete es crear un servicio del sistema operativo a partir de uno o mas .launch files. Si por alguna razón fuera necesario reiniciar el servicio (si por ejemplo algún nodo no responde) se puede usar el siguiente comando desde la terminal:

 $ sudo service mecanumrob stop
 $ sudo service mecanumrob start

Modelado

Primero es necesario definir el sistema de coordenadas del robot (local) y el estático (global).

Se define el marco de referencia local tal que el eje 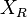$X_R$ corresponde al frente del robot y el eje 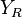$Y_R$ corresponde al lado izquierdo. Además, se define la velocidad angular de las ruedas 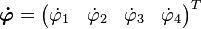$\boldsymbol{\dot{\varphi}} = \begin{pmatrix} \dot{\varphi}_1 & \dot{\varphi}_2 & \dot{\varphi}_3 & \dot{\varphi}_4 \end{pmatrix}^T$ según la ley de la mano derecha tal que una rotación positiva se proyecta en dirección 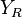$Y_R$ positivo. Luego, se define el marco de referencia global con ejes 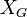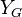$X_G$, $Y_G$. Para encontrar la posición del robot en este marco de referencia global al partir del movimiento de las ruedas se usa el modelo cinemático directo. Por otro lado, para determinar los comandos que se le deben enviar a los motores para alcanzar una cierta velocidad lineal o angular se usa el modelo cinemático inverso.

Modelo Cinemático Directo

El modelo cinemático directo nos permite obtener la velocidad del robot a partir de la velocidad de las ruedas. Definimos la velocidad respecto al marco de referencia local 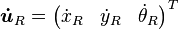$\boldsymbol{\dot{u}}_R = \begin{pmatrix} \dot{x}_R & \dot{y}_R & \dot{\theta}_R \end{pmatrix}^T$. Además queremos encontrar la velocidad respecto al marco de referencia global 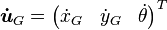$\boldsymbol{\dot{u}}_G = \begin{pmatrix} \dot{x}_G & \dot{y}_G & \dot{\theta} \end{pmatrix}^T$, para poder integrar y así obtener la posición. Para el robot mecanum se tiene que:

$\boldsymbol{\dot{u}}_R = \boldsymbol{J}\cdot\boldsymbol{\dot{\varphi}}$

$\begin{pmatrix} \dot{x}_R\\ \dot{y}_R\\ \dot{\theta}_R \end{pmatrix} = \boldsymbol{J} \begin{pmatrix} \dot{\varphi}_1\\ \dot{\varphi}_2\\ \dot{\varphi}_3\\ \dot{\varphi}_4 \end{pmatrix}$

con

$\boldsymbol{J} = \frac{r}{4}\begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1\\ \frac{1}{l_a + l_b} & -\frac{1}{l_a + l_b} & -\frac{1}{l_a + l_b} & \frac{1}{l_a + l_b} \end{pmatrix}$

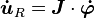
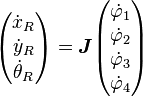
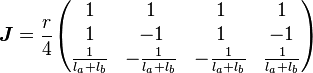
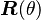
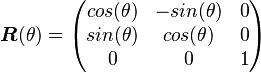
Con esto obtenemos la velocidad lineal y angular del robot respecto al marco de referencia local. Luego, para obtener velocidades globales se debe multiplicar por la matriz de rotación $\boldsymbol{R}(\theta)$

$\boldsymbol{R}(\theta) = \begin{pmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{pmatrix}$

Así, el modelo completo del movimiento del robot es:

$\boldsymbol{\dot{u}}_G = \boldsymbol{R}(\theta)\cdot\boldsymbol{J}\cdot\boldsymbol{\dot{\varphi}}$

$\begin{pmatrix} \dot{x}_G \\ \dot{y}_G \\ \dot{\theta} \end{pmatrix} = \frac{r}{4} \begin{pmatrix} cos(\theta) & -sin(\theta) & 0 \\ sin(\theta) & cos(\theta) & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1\\ \frac{1}{l_a + l_b} & -\frac{1}{l_a + l_b} & -\frac{1}{l_a + l_b} & \frac{1}{l_a + l_b} \end{pmatrix} \begin{pmatrix} \dot{\varphi}_1\\ \dot{\varphi}_2\\ \dot{\varphi}_3\\ \dot{\varphi}_4 \end{pmatrix}$