Julia

Julia es un lenguaje de programación que busca tener la versatilidad y facilidad de uso de Python y la velocidad de C/C++. Julia es un nuevo lenguaje de programación enfocado a ser usado en ambientes científicos. Está construido en torno a ser fácil de escribir como Python pero permaneciendo rápido como C, también se inspira en otros lenguajes como Rust y Lisp.

En esta wiki se cubre la parte introductoria sobre el lenguaje, cubriendo desde lo más básico hasta la utilización del lenguaje para el diseño de sistemas de control. Todas las partes estan complementadas con cuadernos de Jupyter los cuales se pueden descargar de un repositorio de GitHub en: [1]. Comenzando entonces:

Instalación de Julia

Para instalar Julia primero se debe ir a la página oficial lenguaje, luego a su parte de descargas Julia Downloads. Una vez ahí se descarga la versión pertinente al sistema operativo del usuario. Para instalar Julia en Linux se pueden utilizar los siguientes comandos con la versión actual es ese momento (los comandos mostrados aplican para la versión 1.5.0):

wget https://julialang-s3.julialang.org/bin/linux/x64/1.5/julia-1.5.0-linux-x86_64.tar.gz
tar -xvzf julia-1.5.0-linux-x86\_64.tar.gz
ln -s "$PWD"/julia-1.5.0/bin/julia ~/.local/bin/

Una vez instalado Julia se puede correr utilizando el comando "julia" en la terminal de Linux, o abriendo la aplicación instalada en macOS o Windows. Si por alguna razón no se abre o se muestra un mensaje que desconoce el comando, significa que Julia no se ha agregado al PATH y se puede agregar con el siguiente comando:

export PATH="$PATH:/path/to/<Julia directory>/bin"

Donde dice "/path/to/<Julia directory>" se debe cambiar por el lugar de instalación de Julia. Para más información actualizada de los comandos e instalación en cada sistema operativo se puede acceder a [2].

Cómo correr un programa en Julia

Para poder correr un programa en Julia los archivos se guardan con la extensión .jl, por ejemplo programa.jl. Como primer ejemplo se crea un archivo de nombre hola_mundo.jl con la siguiente línea de código solamente:

println("Hola mundo!!")

Una vez creado para correr el programa se corre el siguiente comando en terminal:

julia hola_mundo.jl

En la misma terminal debería aparecer el mensaje:

Hola mundo!!

De esta misma forma se pueden correr todos los programas de Julia, usando el mismo comando con el nombre del archivo del programa deseado.

¿Por qué utilizar Jupyter?

Jupyter es una aplicación de Web la cual entre otras cosas permite el uso de Notebooks los cuales son documentos interactivos donde se pueden explicar conceptos o ejemplos de forma amplia con imágenes y demás en conjunto con código interactivo que se puede correr ahí mismo. Jupyter soporta más de 40 lenguajes diferentes entre ellos Julia [3].

La idea de instalar Jupyter surge dado que permite correr código de Julia de forma interactiva, donde se puede correr cada línea de forma separada si se deseara. Además, de poder agregar explicaciones amplias escritas de varias formas, por ejemplo, LaTeX. La mayoría de partes del tutorial de Julia tendrán un cuaderno de Jupyter específico para cada parte donde se brindan ejemplos y explicaciones de los conceptos explicados acá.

Instalación de Jupyter

Empezando con la instalación, los detalles de instalación de pueden encontrar aquí. En general se requiere de tener instalado conda o pip, luego por medio de estos se puede instalar Jupyter fácilmente. Anaconda o conda es un programa el cual incluye muchos paquetes útiles de Python por tanto es la opción recomendada, las instrucciones de instalación se encuentran en install . Una vez ahí solo se siguen las instrucciones de instalación del sistema operativo respectivo. Por otro lado, pip en general se instala automáticamente con Python, en las versiones recientes.

Para instalar Jupyter con conda se corre el siguiente comando en terminal, en Windows se corre en la terminal de conda:

conda install -c conda-forge notebook

Si se utiliza pip se utiliza este comando:

pip install notebook

Correr Jupyter

Una vez instalado para abrir un cuaderno de Jupyter en blanco se utiliza el siguiente comando en terminal:

jupyter notebook

Cuando se inicia Jupyter se abre sobre el directorio que denomina home donde se pueden abrir cuadernos, o crear uno con la pestaña new. Para poder abrir un cuaderno en específico se puede correr el comando:

jupyter notebook cuaderno_a_abrir.ipynb

Si se desea más información se puede encontrar en la página oficial en la parte de correr cuadernos. Cuando se crea un cuaderno nuevo se puede elegir el lenguaje de programación a utilizar. Antes de poder utilizar Jupyter con Julia se debe instalar el paquete IJulia.

Instalación de Paquetes en Julia

Para instalar paquetes en Julia, el proceso se hace por medio de la terminal de Julia. En Windows y macOS se puede abrir la terminal de Julia corriendo el programa instalado en su computadora, en Linux se puede correr el comando julia en la terminal. Una vez en la terminal de Julia se debe correr el siguiente comando:

using Pkg

Pkg es el manejador de paquetes de Julia y es el encargado de instalar los paquetes que uno desee. Para instalar un paquete solo se debe correr este segundo comando:

Pkg.add("Package Name") 

El primer paquete a instalar se llama IJulia el cual permite usar Julia con Jupyter, para instalarlo se corren estos comandos:

using Pkg
Pkg.add("IJulia")

De la misma forma se pueden instalar paquetes por medio de Jupyter corriendo los mismos comandos anteriores. La mayoría de paquetes soportados por Julia se pueden encontrar en Julia Hub.

• Algunos paquetes utiles que se van a utilizar son:
  • Plots
  • ControlSystems
  • DifferentialEquations
  • Polynomials

Introducción a Julia

Esta parte de introducción del lenguaje sirve como un tutorial de las cosas más básicas que uno puede necesitar para utilizar Julia. Cubre variados temas desde como la sintaxis básica de cómo crear una variable, funciones, estructuras de datos hasta temas como el manejo de archivos de salida y entrada. Todas las partes se pueden encontrar en diferentes cuadernos de Jupyter donde se pueden encontrar más ejemplos e información sobre el tema, además de que en Jupyter si se puede correr el código para ver los resultados de los ejemplos de forma más dinámica.

Uso de variables en Julia

A la hora de utilizar variables en Julia en general no es necesario especificar un tipo ya sea si es una variable entera, flotante u otra. Lo único que se requiere en Julia es de un nombre y el dato a guardar en dicha variable, Julia automáticamente detecta que tipo es o selecciona el tipo más apropiado para este tipo de dato. Por ejemplo:

test = 1
test2 = 1.5
test3 = "Hola mundo!"

En los ejemplos anteriores en Julia la primera variable seria de tipo Int64, la segunda seria de tipo Float64 y la última sería un String. Para saber explícitamente que tipo tiene una variable se puede utilizar la función:

typeof(var) 

Donde var se reemplaza por la variable a revisar. Por otro lado, si un usuario desea definir el tipo de variable a utilizar, por ejemplo, para ahorrar memoria en contadores que nunca sobrepasan algún valor se puede utilizar la siguiente sintaxis para definir un tipo:

test = Int8(10)
test2 = Float32(1.5) 

Lo anterior crea una variable entera de 8 bits en vez de 64 bits como lo haría en general y una variable de tipo flotante con 32 bits en vez de 64. Otra forma para decidir el tipo de un variable solo sirve en variables locales, por ejemplo, dentro de una función. Las variables globales no soportan selección de tipo excepto por el método anterior. La sintaxis para variables locales es por medio del operador :: con la siguiente sintaxis:

function f()
   test::Float32 = 10
end 

Para más información sobre el manejo de tipos de variables en Julia se puede acceder a su manual de tipos oficial.

Como usar comentarios

Para utilizar comentarios en Julia se hace de la siguiente forma:

# Para comentarios de una linea se utiliza #
#= 
  Para comentarios mas largos de varias lineas se utiliza la combinacion #= texto =#
=#

Como imprimir en terminal

En general en Julia a la hora de desplegar información en terminal se utiliza la función:

println()

La función anterior imprime su contenido en la terminal y deja una línea nueva al final, similar a poner \n al final de un mensaje en otros lenguajes. También existe la función:

print()

La función anterior no deja una línea nueva al final, a diferencia del primer método. Un ejemplo de cómo utilizar las funciones anteriores seria:

println("Hola Mundo!")
print("Hola Mundo!")

Continuando, para poder imprimir variables en medio de un mensaje se utiliza el operador $ con la siguiente sintaxis:

num = 10
println("Han pasado $num días")

Donde dice $num se reemplazaría por el valor de 10 en el ejemplo anterior. El operador $ también se puede utilizar para realizar operaciones en medio de la impresión, por ejemplo:

a = 5
b = 10
println("La suma de a + b es $(a+b)")

Lo anterior despliega el mensaje más el resultado de la operación. Por último, la función println() permite impresión de comparaciones directamente como lo siguiente:

println(1 == '1')

Lo anterior mostraría en terminal el resultado de la comparación, en este caso false.

Manejo de Strings

En Julia para declarar un carácter o char se utiliza la comilla simple '.

soy_un_char = 'a'

Por otro lado, para declarar un string se utiliza la doble comilla ".

soy_un_string = "Hola!"

Si se desea crear un string con comillas dentro de él se puede utilizar la triple doble comilla """, por ejemplo:

soy_otro_string = """Acá no hay ningún "error" solo otro string"""

Una característica de los strings en Julia es que pueden ser accesados elemento por elemento como un arreglo:

println(soy_otro_string[5])

Lo anterior imprimiría la letra n del mensaje en terminal. Por otro lado, existen varias formas de combinar strings en Julia, una forma es por el operador *:

string_a = "Soy "
string_b = "un "
string_c = "ejemplo"
string_resultado = string_a * string_b * string_c

Si se corriera el código anterior lo guardado en string_resultado seria la combinación de los tres strings anteriores en ese orden. Por tanto, el resultado sería Soy un ejemplo. La segunda opción es utilizar la función string() de la siguiente manera:

string(string_a, string_b, string_c) 

La función anterior retornaría un string conformado por las tres partes en ese orden.

Estructuras de datos básicos

Esta sección cubre las estructuras más básicas del lenguaje, cada una es importante conocer por sus posibles usos y utilidad en diferentes escenarios.

Dictionaries

Un diccionario consiste en una estructura de datos la cual contiene palabras claves llamadas keywords asociadas a un dato, similar a un libro telefónico. En el libro telefónico la palabra clave o keyword sería el nombre de la persona y dato sería el numero telefónico. Para crear un diccionario se hace de la siguiente forma:

phone_book = Dict("Jose" => 20061234, "Marco" => "23456789", "María" => 98765432)

El ejemplo anterior crea un diccionario con 3 entradas similar a un libro telefónico, Jose y María son palabras claves cuyos valores son Int mientras que el valor asociado a Marco es un string. Los datos de un diccionario pueden ser de diferentes tipos. Para agregar un nuevo valor a un diccionario se utiliza la siguiente sintaxis:

phone_book["Emergencias"] = "911"

Lo anterior crea una nueva entrada llamada Emergencias. Para accesar los datos asociados a una palabra clave en un diccionario se hace de la siguiente forma:

phone_book["Marco"]

Por ultimo, los diccionarios no pueden ser accesados como un arreglo:

phone_book[1] 

Lo anterior no daría la primera entrada del diccionario, sino más bien buscaría un keyword de 1.

Tuples

Los Tuples son similar a un arreglo, su diferencia principal es el hecho que sus contenidos no pueden ser modificados, para crear un Tuple se utilizan los paréntesis ( ), por ejemplo:

tuple = ("Lunes", "Martes", "Miércoles", "Jueves", "Viernes")

Se pueden accesar los índices como un arreglo:

tuple[4] 

Lo anterior retornaría la entrada que dice jueves.

Arrays

Un arreglo es una estructura de datos la cual contiene una serie de datos de forma ordenada la cual puede ser accesada por índices y sus contenidos pueden ser modificados. En Julia a diferencia de otros lenguajes la primera entrada de un arreglo no inicia en la posición 0, en Julia inicia en la posición 1. Para crear un arreglo en Julia se utilizan los paréntesis cuadrados [ ]. Por ejemplo:

array1 = [1,2,3,4,5]
array2 = ["Jose","Marco',"María","Marta"]

En Julia también se pueden crear arreglos con diferentes tipos de variables:

array3 = [1.5, 10,"123"] 

Para accesar un arreglo se hace por medio de su índice:

array1[1] 

Lo anterior retornaría la primera entrada que contiene el número 1. Para modificar el contenido de una entrada se hace de la siguiente forma:

array1[1] = 30

En Julia la función rand() genera números al azar entre 0 y 1. Sin embargo, entre otras cosas permite crear arreglos de longitud n con la siguientes sintaxis:

array = rand(100)

Esto crea un arreglo con números aleatorios entre 0 y 1 de 100 valores.

Funciones Útiles

Algunas funciones útiles para el manejo de arrays son:

• push!(array_or_vector_to_push, arg) Agrega un valor o dato arg al final del arreglo.
• pop!(array_or_vector) Retorna y elimina el ultimo valor de la lista ordenada.
• popat!(array_or_vector_to_pop ,index) Retorna y elimina el valor en algún índice, luego reajusta los contenidos del arreglo.
• insert!(array_or_vector, index, arg) Inserta un valor en la posición indicada.

Nota: Para este tipo de funciones se debe siempre utilizar el operador !, esto se explica en la parte de funciones. En resumen, lo que hace es indicar que las funciones pueden realizar modificaciones a la estructura de datos. Para documentación sobre estas funciones se pueden acceder en la documentación oficial.

Por otro lado, la función rand() permite crear arreglos con valores aleatorios dentro de un rango de valores, por ejemplo un arreglo de tamaño 5 con valores aleatorios entre 0 y 20. Por ejemplo:

arr = rand(0:20, 5)

Lo anterior crea un arreglo de 5 entradas con valores aleatorios entre 0 y 20. La documentación oficial de la función rand() se puede encontrar acá.

Control de Flujo

While loop

Un loop de tipo while es un pedazo de codigo el cual se repite infinitamente hasta que ya no se cumpla alguna condicion (en otras palabras cuando ya no es true). La nomenclatura en Julia para un ciclo while tiene las siguientes partes:

while *condition*

   *codigo*

end

En Julia los while siempre terminan con la palabra end. Un ejemplo de un ciclo while seria:

condition = 0 
while condition < 10 
      condition+=1 
      println("Numero de iteracion $condition")
end 

El codigo anterior se ejecuta mientras el valor de condition sea menor a 10 y se va aumentando en pasos de 1 en 1.

For loop

Similar a un lazo while este tipo de loop se repite siempre y cuando se cumple una condicion. La diferencia principal nace de que se puede controlar cuantas veces ejecutar el codigo dentro del loop. La sintaxis para un for loop en Julia es:

for *variable* in *rango o objeto iterable* 
    *codigo*
end

Un objeto iterable son objetos los cuales se pueden ir revisando sus entradas de forma ordenada, como los tres visto anteriormente. Algunos ejemplos de ciclos for en Julia son:

for i in 1:10 #La sintaxis 1:10 crea un rango de valores los cuales iterar. 
    println("Numero de iteracion $i")
end 

Otro ejemplo con arrays:

arr = rand(1:20, 10)
for i in arr
    println("Contenido del array $i")
end

Ejemplo con dictionaries:

dict = Dict("Max"=>1, "Min" => 10, "Med" => 5)
for i in dict
   println(i)
end

Para recorrer matrices en general se utilizan dos for anidados de la siguiente forma:

matrix = zeros(3,3) 
for i in 1:3
   for j in 1:3
       matrix[i, j] = i + j
   end
end

La funcion zeros(m,n) crea una matriz de tamaño mxn entradas llenas de 0. Los rangos numeros comprenden los limites de filas y columnas de la matriz. Otra forma de realizar lo anterior en Julia es con la siguiente sintaxis:

for i in 1:3, j in 1:3
   matrix[i, j] = i+j
end

Dicha sintaxis permite anidar lazos for de forma mas compacta. Por ultimo, Julia permite algo muy similar a lo que se llama em Python como List Comprehensions, en Julia se llaman Array Comprehensions. Su sintaxis es la siguiente:

arr = [2*x for x in 1:10]

Lo anterior crea un arreglo de 10 entradas donde cada entrada es dos veces su posicion. Tambien se ppuede utilizar para crear matrices:

mat = [x+y for x in 1:5, y in 1:2]

Esto crea una matriz 5x2 cuyas entradas son la suma de sus posiciones.

Condicionales if else

Los condiciones if y else sirven para ejercutar diferentes partes del codigo en base a diferentes condiciones. De forma que si la condicion de if se cumple el codigo se ejecuta, sino se realiza el codigo en else. En Julia esto se ve de la siguiente forma:

if *condition*
   *codigo*
else 
   *codigo*
end

Tambien:

if *condition*
   *codigo*
elseif *condition*
   *codigo*
else 
   *codigo*
end 

Algunos ejemplos son:

num1 = rand(1:10)
num2 = rand(1:10)
if num1>num2
   println("El numero 1 es mayor con valor de $num1")
else
   println("El numero 2 es mayor con valor de $num2")
end

num3 = rand(1:10)
if num1>num2
   println("El numero 1 es mayor con valor de $num1")
elseif num3>num2
   println("El numero 3 es mayor con valor de $num3")
else
   println("El numero 2 es mayor con valor de $num2")
end

Para este tipo de condiciones simples donde solo hay dos caminos como en el primer ejemplo existe otra sintaxis más corta la cual se puede utilizar por medio del operador ?. Por ejemplo, si se desea retornar el número más grande:

num1 = rand(1:10)
num2 = rand(1:10)
(num1 > num2) ? num1 : num2 

Si la condicion se cumple se retorna num1 por ser mayor, caso contrario se retorna num2.

Funciones en Julia

Como declarar una función

En Julia las funciones se pueden declarar de varias formas. La forma más general es la siguiente:

function elevar(x,y)
     x^y
end

Lo anterior crea una función con dos entradas x y y, en Julia en general no es necesario declarar el tipo de variable a recibir. Otro ejemplo:

function f(x,y) 
     x/2+y/2
end

En Julia existe la particularidad de que cuando se hace una función la última línea de código es lo que se toma como retorno, por tanto, no siempre es necesario utilizar el keyword return. Para poder llamar la función se hace de la siguiente forma:

elevar(1,2) 

Existe otra sintaxis para funciones como las anteriores que solo realizan una cosa, reescribiendo las funciones anteriores en la nueva sintaxis:

elevar(x,y) = x^y
f(x,y) = x/2 + y/2

Uso de return en Julia

En Julia como se mencionó antes por defecto se retorna el ultimo valor de una función, sin embargo, si fuera una función más completa surge la necesidad de especificar que dato en particular retornar o si se desea terminar la función en algún punto del código, para ello se utiliza el keyword return.

Si uno desea especificar un tipo de variable en específico a retornar, por ejemplo, un Int8 se hace con la siguiente nomenclatura:

function sum(a,b)::Int8
     return a+b
end 

Como detalle final del uso de return, en Julia se pueden retornar varios valores de una función de forma fácil. Cuando se retornan varios valores lo que en realidad hace Julia es retornar un Tuple con los valores retornados. Esto se hace de la siguiente forma como ejemplo:

function calculadora(x,y)
      return x+y, x-y, x*y, x/y

También en Julia se permite asignar a variables cada parte del return de un solo, por ejemplo:

suma, resta, mult, div = calculadora(3,3) 

Significado del operador !

En Julia muchas de las funciones incluidas con el lenguaje tienen dos versiones, por ejemplo la función sort(). Las segunda versión se llama sort!(), el operador ! lo que significa es que dicha función si modifica los contenidos de su argumento. Por ejemplo si uno le pasa un arreglo a dicha función, lo que retorna en general es una copia del arreglo ordenado, pero cuando se utiliza el operador ! el arreglo como tal, es decir el arreglo original si se modifica.

Uso del operador .

El operador de . en Julia funciona similar a como funciona en Matlab. Su función es que cuando se tiene un arreglo y se llama una función sobre este con el operador . la función se corre sobre cada uno de sus elementos. Este concepto se conoce como Broadcasting en Julia. Por ejemplo, digamos que se desea elevar al cuadrado el valor de todos los elementos de un arreglo:

f(x) = x^2
arr = rand(1:10, 10)
f.(arr)

Otro ejemplo puede ser si se desean pasar todos los elementos de una matriz por alguna clase de función, por ejemplo:

Matrix = rand(1:10, (3,3))

Esta nomenclatura le indica a la función rand que debe crear una matriz 3x3 con entradas aleatorias entre 1 y 10.

matrix_func(x) = x^3/3 - 2x + x
Matrix_B = matrix_func.(Matrix)

Si se desea aún más información y detalles sobre funciones en Julia se puede encontrar en el manual de funciones en Julia.

Utilizacion de paquetes

Para utilizar paquetes en Julia se pueden utilizar los keywords import o using los dos realizan lo mismo cuando se trata de paquetes. Por otro lado, cuando se quiere incluir otro archivo se utiliza el keyword include, por ejemplo asumamos que se tiene un archivo llamado area_figuras.jl este contiene algunas funciones para calcular areas. Para incluirlo se haría nada mas:

include("area_figuras.jl")

Mientras que para llamar ciertos paquetes se puede utilizar la siguiente nomenclatura:

using ControlSystems
import Polynomials 
using Plots

Manejo de Archivos

Como abrir y cerrar archivos

Para poder acceder a un archivo en Julia generalmente se utiliza la función open(). Dentro de su argumento se coloca el camino al archivo en el caso que el archivo se encuentra un folder diferente al actual. Si se desea saber el folder actual donde se está trabajando en Julia se puede utilizar la función pwd().

A la función open() se le pueden pasar varios keywords los cuales indican como se quiere abrir el archivo. Por efecto el archivo se abre solo para lectura.

Tabla de parámetros

Keyword	Función
r	lectura
w	escritura, creación
a	escritura, creación, append
r+	escritura, lectura
w+	escritura, creación, lectura
a+	append, escritura, lectura

Para abrir un archivo se puede hacer:

f = open("test.txt", "r")

Lo anterior abre el archivo para lectura y adjunta a este el nombre f. Para cerrar el archivo se utiliza la función close():

close(f)

Lectura de archivos y uso de bloques do

En Julia generalmente se utiliza un bloque do para el manejo de archivos, esto dado que cuando se termine a de realizar el código deseado sobre el archivo, este usualmente se cierra. Además de que generalmente no se requiere mantener el archivo abierto todo el tiempo que se corre un programa.

Por otro lado, para leer los contenidos de un archivo existen variadas maneras, una es por medio de la función read() a esta función se le indica el archivo a leer y la el tipo de variable a leer. Por ejemplo, si leer un Int un Char, String, etc. La función deja de leer cuando encuentra un valor del tipo requerido.

Por ejemplo, entonces:

open("test.txt", "r") do f
    read(f, String)
end

El código anterior abre el archivo con nombre f. El método anterior tiene el defecto de leer todo el archivo completo, si se desea procesar cada línea del texto por separado se necesita otro método. Para revisar si un archivo está abierto se puede utilizar la función isopen().

isopen(f)

La función read() retorna lo pedido del archivo, en el caso de un String retorna los contenidos de todo el archivo, en el caso de un Int retornaría un valor numérico. Dichos valores pueden ser guardados en variables, por ejemplo, para guardar todo el contenido de un archivo en un String se puede hacer:

open("test.txt", "r") do f
     content = read(f, String)
end 

Lo anterior lee todo el archivo como un String y lo guarda en la variable content. Una particularidad de utilizar bloques do es que las variables utilizadas dentro de estos son locales. Para poder utilizar alguna variable en el resto del programa se debe hacer algo como lo siguiente para que sean globales:

content = open("test.txt", "r") do f
       read(f, String)
end 

Los bloques do funcionan similar a las funciones donde la última línea contiene lo que se retorna del bloque, en el caso anterior entonces el contenido del archivo se retorna y se asigna a content. También se permite retornar más de una cosa, por ejemplo:

line1, line2 = open("test.txt", "r") do f
    line1 = readline(f)
    line2 = readline(f)
    (line1, line2)
end

Lo anterior retorna las dos primeras líneas del documento por medio de la función readline(), cuando se lee una línea se deja un marcador al inicio de la siguiente línea y por tanto se pueden leer líneas de forma continua agregando más funciones readline(). Por otro lado, los valores de las dos líneas se retornan por medio de un Tuple que las contiene. Estas luego se asignan a las variables line1 y line2 respectivamente.

Existen muchas formas para poder leer un archivo línea por línea, un primer ejemplo es por medio de la función eof() dicha función recibe como argumento el archivo y la función indica si ya se ha llegado al final de este por medio de retornar true. Por ejemplo:

open("test.txt", "r") do f
    while(!eof(f))
        println(readline(f))
    end
end

Otra forma de realizar lo mismo es por medio de la función eachline() dicha función retorna un objeto iterable el cual contiene las líneas del archivo. Por tanto, se puede hacer algo como:

open("test.txt", "r") do f 
    for i in eachline(f)
         println(i)
    end
end

Como último ejemplo existe la función readlines() dicha función retorna un arreglo con las líneas del archivo sobre el cual se puede iterar, muy similar al ejemplo anterior.

open("test.txt", "r") do f
    for i in readlines(f)
        println(i)
    end
end

Escritura de archivos

Para la escritura de archivos se utiliza la función write() dentro de dicha función se le indica el archivo a escribir y los datos. Por ejemplo, creando un archivo de prueba:

open("write_test.txt", "w+") do f
    write(f, "Soy un texto de prueba \n")
end 

Lo anterior crea un archivo de prueba y lo llena con el contenido definido, correr varias veces el código no llena el archivo más veces. Si más bien lo que se desea es agregar contenido al archivo en otras palabras hacer append al archivo se debe abrir de la siguiente forma:

open("write_test.txt", "a+") do f
    write(f, "Soy un texto de prueba \n")
end 

En base a la función write() se pueden hacer cosas más complejas como escribir una matriz o una tabla:

nums() = rand(1:10, 3) 
open("write_test.txt", "w+") do f
    for i in 1:3
       n1, n2, n3 = nums()
       write(f, "$n1, $n2, $n3 \n")
    end
end

El código anterior escribe una matriz 3x3 en el archivo de valores aleatorios entre 1 y 10.

Paquete DelimitedFiles

Para le lectura y escrituras de matrices existe el paquete DelimitedFiles. Dentro de este paquete existe la función readdlm a dicha función se le pueden pasar diferentes parámetros de entrada, entre los cuales están:

• El archivo
• El separador de valores, si no se indica se asumen espacios
• El tipo de variable a leer, Float, Int, etc.
• Carácter de final de fila, si no se indica se asume \n

Por ejemplo, para leer la matriz escrita en el ejemplo anterior se puede hacer fácilmente de la siguiente manera:

using DelimitedFiles
readdlm("write_test.txt", Int) 

Luego de incluir el archivo en nuestro programa en Julia se puede utilizar la función readdlm(), dicha función lee la matriz con entradas de tipo Int. Dentro de este paquete también existe la función writedlm() con dicha función se pueden escribir fácilmente matrices, arreglos y otras cosas de forma fácil. A dicha función se le indica el archivo, vector o matriz u otro y como opcional se puede elegir el delimitador entre cada valor. Por ejemplo, para escribir una matriz aleatoria con delimitador de espacios se puede hacer como:

writedlm("write_test.txt", rand(5,5), ' ')

Para escribir un arreglo:

writedlm("write_test.txt", rand(1:10, 10), ' ')

Plotting en Julia

En este parte se cubren las partes más importantes para poder graficar en Julia. Para ello la guía se basa en el uso del paquete básico Plots, en base a este paquete se implementan muchos otros y por tanto se utiliza como base. Julia permite grandísima variedad en sus plots, principalmente por la facilidad de poder utilizar diferentes backends. Dado que no se puede cubrir el mar de posibilidades se tratan de cubrir las características más útiles que se pueden necesitar en el día a día. Dentro de los temas a explicar se explica el paquete Polynomials, dicho paquete permite ingresar polinomios a Julia de forma fácil, se piensa explicar el paquete dado que nos permite obtener datos a graficar.

Plotting Básico

Para poder empezar a realizar plots en Julia primero se debe instalar el paquete Plots por medio de las siguientes instrucciones en la terminal de Julia:

using Pkg
Pkg.add("Plots")
Pkg.add("Polynomials")

De paso se instala el paquete Polynomials que se piensa explicar después. Luego se debe llamar el paquete para poder utilizarlo usando:

using Plots

La ventaja de usar el keyword using en vez de import es que cuando se llamen funciones del paquete llamado no se debe agregar el nombre de este al llamado de la función.

Line Plots

El tipo más básico de Plots en Julia son los gráficos de línea y es el tipo por defecto que se utiliza a menos que se indique otra forma por medio de los atributos que se verán más adelante. Para crear un gráfico se utiliza la función plot() a dicha función se le indican los ejes, por ejemplo:

x = 1:10
y = rand(1:10, 10)
plot(x, y)

Lo anterior genera un gráfico como:

También se pueden graficar más de una línea en la gráfica utilizando plot!() dicha función modifica el Plot actual y agrega otra línea a graficar, en este caso sería el anterior:

z = rand(1:10, 10)
plot!(x, z)

En el caso que hubieran más de un Plot actual se puede asignar un identificador a cada uno y luego se le indican los valores a graficar en ese mismo plot, por ejemplo:

grafica = plot(x, y) 
plot!(grafica, x, z)
w = rand(1:10, 10)
plot!(grafica, x, w)

Otra forma más compacta de agregar varias series de datos seria indicar el eje x de todos los datos y luego solo indicar los diferentes ejes y a graficar de la siguiente forma: grafica2 = plot(x, [y,z,w])

Que son backends en Julia

En Julia por lo general se utiliza el paquete `Plots` para graficar, sin embargo, este no es una librería como tal sino una interfaz la cual utiliza diferentes librerías para graficar. Lo que el paquete hace es interpretar los comandos de otras librerías, la librería que se utiliza para generar los plots se llama backend. La ventaja de esto es que se pueden utilizar diferentes librerías para realizar plots bajo la misma sintaxis.

En general sino se escoge un backend el paquete utiliza alguno por defecto que encuentre instalado. Para poder instalar nuevos backend se pueden instalar similar a un paquete:

using Pkg
Pkg.add("Name")

Algunos backends populares son:

• Plotly
• GR
• PyPlot
• PlotlyJS

Para las futuras imágenes se va a utilizar los backends GR y PyPlot, para instalarlos se pueden correr los siguientes comandos en la terminal de Julia:

Pkg.add("GR")
Pkg.add("PyPlot")

Cada uno de ellos tienen sus propias ventajas y desventajas, a los usuarios de Python se les permite utilizar PyPlot en Julia de forma fácil. Los diferentes backends tienen diferentes atributos que pueden utilizar, dicha lista se puede encontrar en la documentación oficial. Para poder utilizar un backend se utiliza la siguiente sintaxis antes de graficar:

GR()

La página de documentación de Julia tiene una tabla resumen de las mejores características para cada tipo de backend y se invita a revisar cual es que se desea.

Atributos

A un buen grafico siempre es importante ponerle las partes más básicas como:

• Nombres de los ejes
• Leyenda
• Título del gráfico

Todas estas propiedades se agregan y modifican por medio de los atributos que uno puede utilizar para los gráficos. Existen gran variedad de atributos diferentes, acá solo se cubren algunos de ellos que se consideran los más relevantes para un uso general.

Comenzando el título, para agregar un título a un plot se utiliza el keyword title, para agregar los nombres de las leyendas se utiliza el keyword label. Por ejemplo, entonces:

p = plot(x, y, title = "Plotting en Julia", label = "Línea 1")

Cuando se tienen varias series de datos para modificar su nombre en la leyenda se debe poner el nombre de cada una en orden separados por un espacio, por ejemplo:

plot(x, [y,z], label = ["Línea 1" "Línea 2"])

Para agregar nombres a los ejes se tienen dos keywords xlabel y ylabel, modificando el ejemplo anterior:

plot!(xlabel = "Eje x")

Otra manera de modificar el plot actual es por medio de utilizar el keyword de como si fuera un función de la forma:

ylabel!("Eje y")

La nomenclatura anterior solo sirve para ciertos atributos. Los comandos anteriores entonces resultan en un gráfico como:

Otro atributo interesante es poder cambiar el grosor de las líneas por medio del keyword lw, creando un nuevo gráfico:

plot(x, [w,z], label = ["Linea 1" "Linea 2"], lw =4)

Tipos de Línea

Continuando con atributos para las líneas, se puede cambiar el estilo de línea por medio del alias ls o linestyle:

• dot
• solid
• dash
• dashdot

Es importante revisar cuales atributos y características están implementadas en cada backend que se esté utilizando.

Algunos ejemplos de líneas son:

plot(x, [w,z], label = ["Línea 1" "Línea 2"], lw =4, ls = :dot)

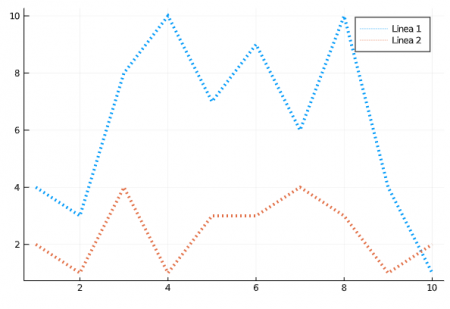
plot(x, [w,z], label = ["Línea 1" "Línea 2"], lw =4, ls = :dashdot)

El color de todas las líneas de puede cambiar por medio del alias c o el keyword seriescolor:

plot(x, [w,z], label = ["Línea 1" "Línea 2"], lw =4, c = :green)

Si más bien lo que se quiere es darle un color especifico a cada línea se puede hacer algo como lo siguiente de forma manual:

plot(x, w, label = ["Línea 1" "Línea 2"], lw =4, c = :red3)
plot!(x,z, lw = 4, c = :darkblue)

Lo cual da como resultado:

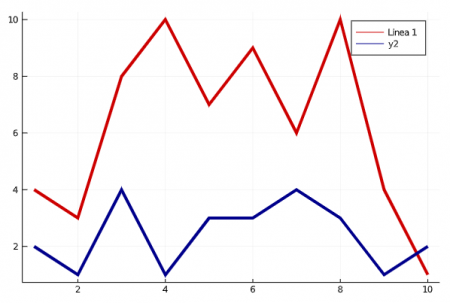
Para mas detalles de cuales colores se pueden utilizar y demás información se puede encontrar en Julia Colors.

Tipos de graficas

Otro atributo interesante que se puede modificar es el tipo de grafico que se está realizando, por ejemplo, existen los tipos: steppre y scatter, entre otros. Diferentes tipos se pueden utilizar para diferentes situaciones, a continuación de muestra cómo utilizarlos y algunos ejemplos:

plot(x, w, label = ["Linea 1" "Linea 2"], lw =4, st = :scatter)

plot(x, w, label = ["Linea 1" "Linea 2"], lw =4, st = :steppre)

Existen gran variedad de estilos diferentes que se pueden utilizar, en esta guía solo se cubren algunos. Todos los tipos soportados se puede encontrar en la página de atributos para las series en la sección de 'series type'. También se pueden definir el tipo de grafica de forma externa usando el nombre el tipo en vez de plot, por ejemplo:

histogram(x, y)
scatter(x, y)
heatmap(x, y)

Solo algunos tipos se pueden definir de esta forma.

Por ejemplo:

histogram(x, w)

Atributos para los Ejes

Para poder escoger los límites de los ejes se puede utilizar el atribulo lim, de la forma:

data = rand(10)
x_line = 1:10
plot(x_line, data, xlims = (0,20), ylims = (0,5), lw =4)

Al igual que algunos otros atributos se puede modificar por si solo de forma explícita por medio de xlims!().

xlims!(0,10)

También se puede decir la escala de los ejes de forma fácil, sin embargo, se debe recordar que algunos backends soportan solo algunos tipos de escalas. Por ejemplo, en general existen:

• :log10
• :ln
• :log2

plot(x_line, data, lw =4, scale = :log10)

El ejemplo anterior cambia la escala de todo el grafico, para poder cambiar solo la escala de un eje se puede utilizar el keyword xscale para solo cambiar la escala del eje x. Existen más atributos como minorgrid, o grid los cuales se pueden habilitar y deshabilitar respectivamente:

plot(x_line, data, lw =4, xscale = :log10, minorgrid = true, grid = false)

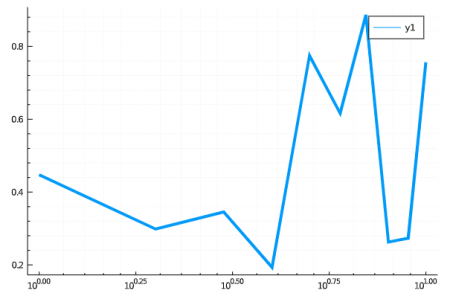
El ejemplo anterior muestra las diferencias al modificar dichos atributos. Se puede hacer cosas más interesantes con `grid` como solo habilitar líneas hacia ciertos ejes, o cambiar el tipo de línea o inclusive aumentar o disminuir su grosor. Todos los atributos relacionados con los ejes o axis se puede encontrar en la página de axis attribute. Por ejemplo:

plot(x_line, data, lw =4, scale = :log10, grid = :x)

Otros atributos que se pueden modificar para los ejes son, por ejemplo:

• xlabel modifica el nombre del eje
• xlims modifica los límites del eje
• xticks cambia cada cuanto se muestra un valor en el eje x, se modifica por medio de un rango
• xscale modifica la escala del eje en especifico
• xflip da vuelta al eje x, como un espejo
• xtickfont modifica el tipo de letra de los números desplegados en el eje, también puede modificar el tamaño

Por ejemplo, modificando todo lo anterior:

plot(rand(10),
   xlabel = "x label",
   xlims = (0,10),
   xticks = 0:0.5:10,
   xscale = :identity,
   xflip = true,
   xtickfont = font(5, "Courier")
)

En el caso anterior no es necesario darle un rango al eje x, Julia automáticamente crea un rango 1:10 para el set de valores. Existen también las versiones para el eje y y z para cada atributo, además se pueden cambiar los parámetros de todos los ejes por medio del keyword axis.

Marcadores

En Julia existentes diferentes opciones de marcadores que se pueden utilizar y modificar según los intereses de uno. Por ejemplo, se pueden escoger:

• Tipo de marcador con markershape
• Tamaño del marcador con markersize
• Intensidad del marcador con markeralpha
• Color del marcador con markercolor
• Grosor de las líneas del contorno del marcador markerstrokewidth
• Intensidad de las líneas del contorno markerstrokecolor
• Estilo de las líneas del contorno markerstrokestyle

Dentro de algunos tipos de marcador hay:

• hexagon
• circle
• diamond
• xcross
• cross
• pentagon
• star4
• star6

Entre otros que se pueden encontrar en la documentación en la parte de atributos para markershape. A continuación se muestran algunos ejemplos de cómo los diferentes atributos modifican los gráficos.

scatter(y,
   markershape = :hexagon,
   markersize = 5,
   markeralpha = 0.6,
   markercolor = :green,
   markerstrokewidth = 2,
   markerstrokealpha = 0.2,
   markerstrokecolor = :black,
   markerstrokestyle = :dot
)

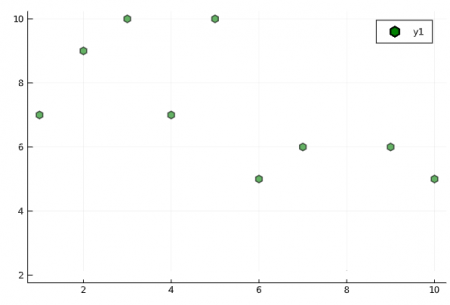
plot(1:1:100, (x)-> x^2,
  markershape = :cross,
  markersize = 3,
  markeralpha = 0.5,
  markercolor = :red,
  markerstrokewidth = 2,
  markerstrokealpha = 0.2,
  markerstrokecolor = :black,
  markerstrokestyle = :dot
)

Nótese que en el caso anterior el eje y se rellenó con una función anónima o una función lambda de Python. Julia automáticamente reconoce que es una función y ejecuta sobre ella el rango de valores ingresados para generar la gráfica. Continuando con un par de ejemplos más:

plot(1:1:10, [(x)-> (x^2+x), (y) -> y^2],
linecolor = :black,
markershape = [:star4, :diamond],
markersize = 5,
markeralpha = 0.6,
markercolor = [:red, :blue],
markerstrokewidth = 2,
markerstrokealpha = 0.2,
markerstrokecolor = :black,
markerstrokestyle = :dot
)

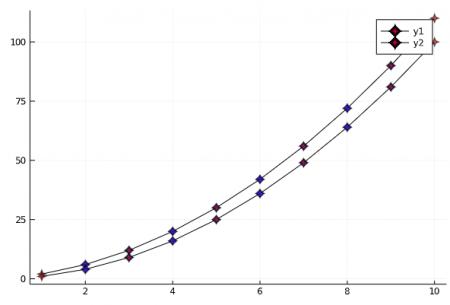
plot(1:1:10, (x) -> x+10,
linecolor = :grey,
markershape = :star4,
label = "recta 1",
markersize = 5,
markeralpha = 0.6,
markercolor = :brown,
markerstrokewidth = 2,
markerstrokealpha = 0.2,
markerstrokecolor = :black,
markerstrokestyle = :dot
)
plot!(1:1:10, (y) -> y/2 + 10,
st = :scatter,
label = "recta 2",
linecolor = :black,
markershape = :diamond,
markersize = 5,
markeralpha = 0.6,
markercolor = :cyan,
markerstrokewidth = 2,
markerstrokealpha = 0.2,
markerstrokecolor = :black,
markerstrokestyle = :dot)

Funcionamiento de subplots

Los subplots son muy útiles en algunos casos. Imaginemos que tenemos 4 sets de datos que representan por ejemplo cuatro respuestas al escalón de 4 sistemas, probablemente queramos ver graficado dichos comportamientos. Pero puede ser un poco difícil de ver los resultados correctamente si todos están juntos en una misma gráfica, por tanto, se pueden utilizar subplots.

En base al ejemplo anterior para solucionarlo fácilmente en Julia se puede utilizar el comando layout:

#Primero creamos 4 "sistemas"
sis1(x) = x+x/2
sis2(x) = x-x/2
sis3(x) = x^2 - x
sis4(x) = x
#Sobre los 4 "sistemas" aplicamos un rango de valores y graficamos
plot(1:1:30, [sis1, sis2, sis3, sis4], layout = (2,2))

El uso de layout permite poder decir de forma fácil de qué forma queremos que la información sea desplegada, en este caso se pide una matriz 2x2 donde cada entrada es una gráfica. Dependiendo de la forma que se indica el layout se puede generar diferentes formas:

plot(1:1:30, [sis1, sis2, sis3, sis4], layout = (4,1))

Para poder agregar más detalles como títulos y demás se puede seguir el siguiente ejemplo donde también se combinan diferentes tipos de gráficos:

p = scatter(1:1:30, sis1, title = "sis1")
p2 = histogram(1:1:30, sis2, title = "sis2")
p3 = plot(1:1:30, sis3, title = "sis3", lw = 4)
p4 = plot(1:1:30, [sis2,sis3,sis4], title = "Varios sistemas", linestyle = :dash,
   linecolor = [:purple :green :darkred :darkblue])
plot(p,p2,p3,p4, layout = (2,2))

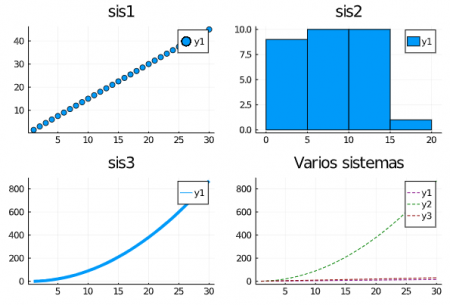
Como detalles finales sobre el uso de layout se tiene el uso del constructor grid este permite modificar de forma facil que tanto espacio se le da a cada gráfica, por ejemplo:

plot(p,p2,p3,p4, layout = grid(4,1 , heights = [0.1, 0.2, 0.3, 0.5]))

Por ultimo, si se desean esquemas mas particulares se puede utilizar el macro @layout de Julia para crear formas diferentes layouts. Tomando el ejemplo de la documentación oficial.

l = @layout [
   a{0.3w} [grid(3,3)
            b{0.2h}  ]
]
plot(
   rand(10, 11),
   layout = l, legend = false, seriestype = [:bar :scatter :path],
   title = ["($i)" for j in 1:1, i in 1:11], titleloc = :right, titlefont = font(8)
)

Otros temas

Esta sección cubre algunos temas que se salen de las bases de graficar.

Scripting

Cuando se escriben scrips donde se generan varios gráficos, ya sea para un proyecto o tarea, dependiendo de la forma que se está corriendo el programa puede que los plots que uno crea no aparezcan. Esto sucede porque a diferencia de trabajar en algo como Jupyter donde se pueden correr líneas de código en celdas, en un programa de Julia solo desplegaría la última línea de un programa. Para poder decirle a Julia que debe desplegar un gráfico se debe utilizar la función display(). Por ejemplo:

display(plot(rand(10), rand(10)))

O también si se tiene un plot con nombre:

p = plot(x,y)
display(p)

El utilizar el la función display() le indica a Julia que debe desplegar el output de ese código, en el caso de plot() seria la gráfica como tal.

Otros tipos de Plots

Julia permite gran variedad de plots los cuales pueden ser útiles en diferentes escenarios, como por ejemplo imagínenos que necesitamos graficar una superficie:

Un ejemplo más visualmente interesante es crear un plot del tipo surface que sirve para casos en 3d con superficies. Tomando una función

$\sin 5x\cdot \frac{cos5y}{5}=z$

La cual se grafica de -1 a 1 con 200 pasos en sus ejes. Para crear el rango de valores se utiliza la función `range()`. La documentación de la función se puede encontrar acá.

Continuando con el ejemplo, una vez que se tienen los rangos de valores a evaluar en Julia se tiene la facilidad de que en estos casos el eje z de la función a graficar puede ser la función misma como la siguiente sintaxis:

plot(x_values, y_values, fuction(x_values,y_values) ...)

En Julia utilizando la sintaxis anterior automáticamente se evalúan los valores de x y y en la función y ese valor es el que grafica en el eje z de forma fácil. El ejemplo entonces se puede graficar muy fácilmente con lo siguiente:

x = y = range(-1,1, length = 200)
f(x,y) = sin(5x)*cos(5y)/5
plot(x,y,f, st = :surface)

Uso de temas

Julia posee un paquete llamado PlotThemes el cual como dice su nombre puede construir gráficos utilizando temas que este paquete posee. El repositorio oficial del paquete se encuentra en PlotThemes.jl. Algunos de los temas que se soportan son:

• :dark
• :juno
• :lime
• :sand

Entre otros, a al hora de elegir un tema de utiliza el comando theme(), los plots siguientes a este comando tomaran el tema elegido. Para volver al tema original de utiliza el atribulo :default de la forma theme(:default). Para utilizarlo temas entonces, primero se llama el paquete:

using PlotThemes
theme(:dark)
plot(rand(100))

Paquete Polynomials

Entre los muchos paquetes de Julia existe el paquete Polynomials dicho paquete permite la utilización de polinomios de manera muy simple. Este paquete habilita el manejo de polinomios de una sola variable, para polinomios de más variables existe el paquete MultivariatePolynomials.jl. Continuando entonces, para poder crear un polinomio se puede hacer de dos formas:

La primera forma es por medio de la función Polynomial() donde se le pasan los coeficientes de las variables de izquierda a derecha para ir aumentando su potencia. Por ejemplo:

Polynomial([1,2,3,4])
> 1 + 2x + 3x^2 + 4x^3

Si se desea crear un polinomio que no sea con la variable x se puede indicar la variable a utilizar por medio de la siguiente sintaxis:

Polynomial([1,2,3,4], :s)

El segundo método consiste en crear el polinomio en base a sus raíces, es decir si solo hay una raíz -2 el polinomio seria en ese caso x+2. Para ello entonces se usa la función fromroots() de la siguiente forma:

fromroots([-2])
fromroots([-2,1,3])

Para evaluar nuestro polinomio anterior basta con evaluar su nombre como si fuera un función por ejemplo:

pol = Polynomial([1,2,3,4])
pol(10)
> 4321

Antes de continuar con las demás capacidades de este paquete, parte de la idea de incluir la explicación de este es que se puede utilizar para realizar graficas. Utilizando la función anterior de evaluar el polinomio en conjunto con un poco de código en Julia podemos graficar fácilmente el polinomio. Por ejemplo:

pol_y_values = [pol(i) for i in 1:10]
plot(1:10, pol_y_values, label = pol)

La utilización de Array Comprehensions de Julia permite rápidamente poder graficar polinomios como el anterior. Se pueden también graficar varios polinomios siguiendo el siguiente ejemplo:

pol2 = Polynomial([1,-2,-4,8])
pol2_vals = [pol2(i) for i in 1:10]
plot(1:10, [pol_y_values, pol2_vals], label = [pol pol2], lw = 4, linecolor = [:red :blue])

Continuando con las capacidades del paquete, este implemente variadas operaciones de polinomios como los son:

• Suma
• Resta
• División
• Multiplicación

Dichas operaciones anteriores se pueden utilizar sobre varios polinomios siempre y cuando tengas la misma variable, usualmente x. Por ejemplo:

pol1+pol2
pol1-pol2
pol1 * pol2
3pol1

La división es un caso un poco particular dado que para dividir dos polinomios se debe usar la función div() la cual retorna el resultado de la división nada más. Si se desea el residuo de la división se puede usar rem() lo cual solo retorna el residuo, si se desea ambos el residuo y la división se puede utilizar divrem(). Por otro lado, si lo que se quiere es dividir un polinomio con un número se puede hacer normalmente por medio del operador /.

div(pol1,pol2)
rem(pol1,pol2)
divrem(pol1,pol2)

Otra funcionalidad incluida en este paquete es la posibilidad de integrar y derivar los polinomios por medio de las funciones derivative() y integrate().

derivative(pol1)
integrate(Polynomial([1,1,-1]))

Por último, también se incluye la funcionalidad de encontrar las raíces de los polinomios por medio de la función roots():

roots(Polynomial([1,0,3,0,9]))

Sistemas de Control

En esta parte se cubre el uso del paquete ControlSystems.jl el cual contiene muchas de las herramientas necesarias para el diseño y análisis de sistemas de control. Por el momento, es uno de los paquetes más robustos en esta parte y es el recomendado actualmente. Acá se trata de explorar las capacidades importantes de este paquete, pero se invita al lector a leer más sobre las capacidades de este en la documentación oficial. También, se invita al lector a practicar las herramientas acá expuestas dado que no cubren todas las capacidades de este paquete.

Lo primero antes de poder utilizar este paquete es instalarlo por medio de la terminar de Julia, con los siguientes comandos:

using Pkg
Pkg.add("ControlSystems")

Luego se debe incluir en nuestro programa, es generalmente mejor utilizar el keyword using al llamar un paquete para no tener que llamar su namespace cada vez que se quiera utilizar.

Creación de Funciones de Transferencia

La utilización de funciones de transferencia es una de las bases en los sistemas de control más importantes, es esencial poder manejar y utilizar esta herramienta matemática. Una función de transferencia modela la relación entrada salida del sistema:

$H(s)=\frac{Y(s)}{X(s)}$

Ahora en Julia tomemos por ejemplo la siguiente función de transferencia:

$F(s)=\frac{s+1}{s^2+5s+6}$

Separando sus partes en denominador y numerador la función de transferencia se crea con la siguiente función: tf(num, den)

fs = tf([1,1], [ 1, 5, 6]) 

Otro ejemplo:

$F(s)=\frac{s+2}{3s^3+5s^2+6s}$

fs2 = tf([1,2], [3,5,6,0])

Existe una segunda forma de ingresar una TF y es por medio de su representación zpk que significa la representación en ceros, polos y ganancia. Para construir una TF por medio de esta representación se utiliza la función zpk() de la forma zpk(ceros, polos, ganancia). Construyendo el primer ejemplo:

fs = zpk([-1],[-2,-3], 1)

Es importante mencionar que los dos métodos de creación permiten obtener una función de transferencia, sin embargo, dependiendo del método que se utiliza para crearla, el tipo resultante es diferente. Para convertir de un tipo al otro se puede hacer:

tf(fs)

Este paquete también soporta la siguiente nomenclatura para crear funciones de transferencia, muy similar a Matlab:

s = tf("s")
P = (s+1.0)/((s+1)*(s+2)^2)

Como ultimo comentario, puede ser útil algunas veces utilizar números flotantes en vez de enteros a la hora de declarar una función de transferencia. Existe otra función constructora llamada feedback() dicha función permite construir las siguientes formulas:

$\frac{L}{L+1}$

$\frac{P1}{1+P1\cdot P2}$

Dependiendo de cómo se utiliza, por ejemplo feedback(sys) retorna la primera y feedback(P1,P2) construye la segunda.

Ingreso de Modelos en Variables de Estado

Un modelo en variables de estado consiste en cuatro matrices que se conocen como A, B, C y D, por medio de la función ss(A,B,C,D) se puede ingresar nuestro sistema en variables de estado. Por ejemplo:

state_model = ss([5 0; 5 0], [2 ; 2], [3 3], [0])

Funcionalidades para graficar

El paquete `ControlSystems.jl` posee variadas opciones relevantes en el diseño de sistemas de control. Entre ellas se pueden encontrar los siguientes tipos de gráficos o funciones:

bodeplot()
gangoffourplot()
impulseplot()
marginplot()
nyquistplot()
pzmap()
stepplot()
rlocusplot()
pidplots()

Diagramas de Bode

Siguiendo el orden anterior entonces primeros tenemos el diagrama de bode a una función de transferencia o modelo en variables de estado. Por ejemplo, tengamos la siguiente función de transferencia de lazo cerrado: $1+L(s)=5\frac{s+1}{(s+1)(s+2)}$

La función `setPlotScale()` permite escoger la escala de magnitud para el diagrama de bode, permite dB o log10.

sys = zpk([-1],[-1,-1],5)
bodeplot(sys)

Lo anterior general algo como:

Es importante mencionar que se le pueden agregar detalles a las gráficas por medio de los mismos comandos vistos en el cuaderno de Plots.jl, dado que este paquete es que se utiliza para realizar las gráficas. Otra funcionalidad es poder deshabilitar el diagrama de fase y graficar más de un sistema al mismo tiempo.

bodeplot(sys; plotphase=false)

También, se pueden ver dos sistemas al mismo tiempo, por ejemplo:

sys2 = tf(1.0, [1,2,3])
bodeplot([sys,sys2], title= "Ejemplo de dos Sistemas")

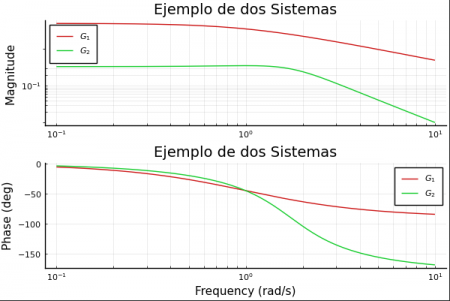
Gang of Four

Este nombre se le da a un conjunto de 4 ecuaciones importantes en el diseño de sistemas de control. Las 4 ecuaciones son las siguientes:

• $\frac{PC}{1+PC}$ Función de sensibilidad complementaria
• $\frac{P}{1+PC}$ Load Disturbance sensitivity function
• $\frac{C}{1+PC}$ Noise sensitivty function
• $\frac{1}{1+PC}$ Funcion de sensibilidad

El grupo de funciones anterior describen diferentes respuestas del sistema de control y todas se pueden graficar rápidamente por medio de la función gangoffourplot() con la siguiente forma:

gangoffour(Plant, Controller)

Si lo que se desea más bien es obtener todas las funciones anteriores de forma individual se puede llamar la función gangoffour(Plant, Controller) y lo que retornará será algo similar a un tuple con las cuatro funciones de transferencia.

gangoffourplot(sys,sys2)

Impulse Plot

Esta función como dice su nombre dará como resultado la gráfica de respuesta el impulso del sistema. Por ejemplo:

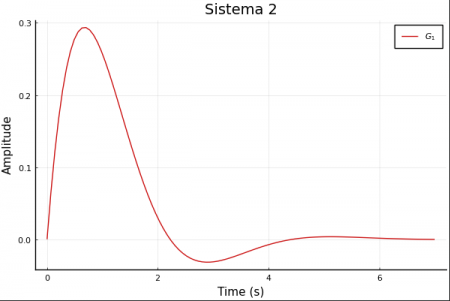
impulseplot(sys; title="Sistema 1")

impulseplot(sys2; title= "Sistema 2")

Margin Plot

Por medio de la función marginplot() se grafican todos los márgenes de fase del sistema y se despliegan los valores resultantes para estos. Por ejemplo:

sys3 = 3tf([1.0],[4,5,5,1])
marginplot(sys3)

Diagramas de Nyquist

El diagrama de Nyquist permite conocer la estabilidad de un sistema a lazo cerrado a partir de su cantidad de encierros en el punto -1.

nyquistplot(sys3)

Los círculos que se observan en la gráfica, se llaman círculos de ganancia. Estos pueden ser deshabilitados por medio del argumento gaincircles=false

Mapa de Polos y Ceros

La función pzmap() grafica el mapa de ceros y polos de la función de transferencia o modelo en variables de estado.

pzmap(state_model)

pzmap(sys3)

Step Plot

Para realizar un diagrama de la respuesta el escalón de un sistema se puede utilizar la función stepplot().

stepplot(sys)

Diagrama LGR o root locus

El diagrama LGR de un sistema de puede graficar por medio de la función rlocusplot() esta funcion tiene dos parámetros, el sistema como tal y un rango de ganancias a utilizar para el LGR. Si no, se indica ningún rango de ganancias la función utiliza un valor por defecto. Además, si se desea un algoritmo más complejo para el rango por defecto de ganancias se puede llamar el paquete OrdinaryDiffEq.jl y al llamar la función este utilizara este paquete para un nuevo algoritmo. También, se le puede pasar un valor de ganancia máxima al utilizar el paquete anterior. Para utilizar la función entonces:

rlocusplot(sys, rango de ganancias k)

Ejemplo:

rlocusplot(sys3)

PID Plot

Existe una herramienta la cual permite obtener las gráficas de un sistema de control el cual incluye la planta P y el controlador C de tipo PID. Primero, sin embargo, existe la función pid() la cual retorna un controlador PID de tipo paralelo por defecto con los parámetros que uno le ingrese:

C = pid(; kp = 0, ki =0, kd = 0, time = false, series = false) 

Como se ve, a la función se le pasan los valores en forma de ganancia para los parámetros del controlador, el argumento time permite indicar si lo que se ingresan son ganancias o constantes de tiempo. Mientras que series permite crear un controlador pid serie en vez de paralelo.

C = pid(kp = 2, ki =4.0, kd = 2, time = true, series = false)
C = pid(kp = 2, ki =4.0, kd = 2, time = false, series = true)

Por otro lado, se tiene la función pidplots() la cual ahora si graficar el comportamiento del sistema de control como tal. Sus parámetros de entrada posibles tienen la siguiente forma:

pidplots(P, args...; kps = 0, kis = 0, kds = 0, time = false, series = false)

Donde se recibe la planta a controlar, los parámetros de un controlador o los parámetros de los controladores a probar que se pueden ingresar por medio de vectores que deben todos ser del mismo tamaño. Los args... indican las gráficas a realizar y soportan:

• :gof - Gang of Four
• :nyquist
• :controller
• :pz

pidplots(sys3, :controller, :nyquist; kps =[2,1,1], kis =[1,2,3], kds =[2,1,3])

pidplots(sys3, :gof; kps =[2,1,1], kis =[1,2,3], kds =[2,1,3])

Funciones Útiles

Este paquete incluye varias herramientas de análisis para los sistemas de control, si se desea explorar la lista entera de estas capacidades de pueden encontrar en la parte de análisis de la documentación oficial. Se incluyen, por ejemplo:

• damp() y dampreport()
• dcgain()
• margin()
• pole()
• zpkdata()

Siguiendo el orden anterior, la función damp() y dampreport() sirven para calcular los valores de frecuencia natural, factor de amortiguamiento de los polos, además retorna los polos. damp() retorna los valores de la siguiente forma:

wn, fa, ps = damp(sys)

Mientras que dampreport() calcula las mismas cosas, pero solo las despliega.

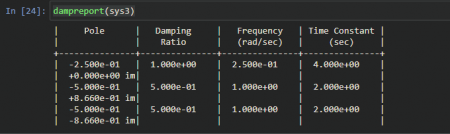
Continuando dcgain() retorna la ganancia dc del sistema. margin() es una función la cual retorna 4 valores que incluyen los valores de frecuencia de corte en ganancia, margen de ganancia, frecuencia de margen de fase y margen de fase. Los retorna de la siguiente forma:

La función pole() simplemente calcula los polos del sistema. Por último, la herramienta zpkdata() retorna los valores de ceros, polos y ganancias del sistema de la siguiente forma:

z, p, k = zpkdata(sys)

Herramientas de Análisis

Existen varias herramientas de análisis y diseño dentro de este paquete, viendo algunos de ellos se tiene:

• loopshapingPI()
• stabregionPID()

Comenzando con loopshapingPI() esta funcion permite obtener los parámetros de un controlador PI. Permite que un valor de frecuencia wp de mueva a un valor $rl{e}^{i{O}_l}$ , donde 𝑟𝑙 y 𝜙𝑙 son parámetros de entrada:

kp, ki, C = loopshapingPI(P, wp; ϕl, rl, phasemargin, doplot = false)

Donde phasemargin hace que si existe un valor de 𝜙𝑙 el Angulo de la curva se mueve a un valor de 180 - phasemargin. doplot indica si desplegar el diagrama de nyquist y gof del sistema.

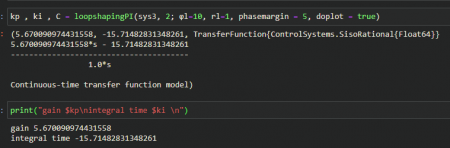
Si por alguna razón no sirviera el comando doplot se puede utilizar algo como lo siguiente para tener esos gráficos.

gangoffourplot(sys3,[tf(1),C]) |> display
nyquistplot([sys3, sys3*C], xlims = (-5,5), ylims = (-5,5)) |> display

Continuando con stabregionPID() esta función retorna los segmentos de la figura que están en el límite de la estabilidad para una planta P. El controlador se asume con la forma 𝑘𝑝+𝑘𝑖/𝑠+𝑘𝑑𝑠 . Los parámetros de entrada son:

fig, kp, ki = stabregionPID(P, kd = 0, doplot=true)

Ejemplo de Análisis

Los siguientes ejemplos sirven para observar las capacidades de este paquete, la mayoría son inspirados de la documentación oficial. Tomemos la siguiente planta:

P = tf(1,[1,1])^4
gangoffourplot(P, tf(1)) #tf(1) es para tener como C un controlador de ganancia uno

Ahora asumamos que por alguna razón del destino queremos que a frecuencia w = 0.8 rad/s queremos que el margen de fase sea de 60 grados, podemos obtener el controlador que logra cumplir dicho requerimiento de forma fácil de la siguiente forma:

wp = 0.8
kp, ki, C = loopshapingPI(P, wp, phasemargin = 60)

Lo anterior retorna un controlador PI que cumple la condicion deseada. Para poder comparar el controlador original con el nuevo se puede hacer de la siguiente forma:

p1 = gangoffourplot(P, [tf(1), C]);
p2 = nyquistplot([P, P*C], ylims=(-1,1), xlims=(-1.5,1.5));
Plots.plot(p1,p2, layout=(2,1), size=(800,800))

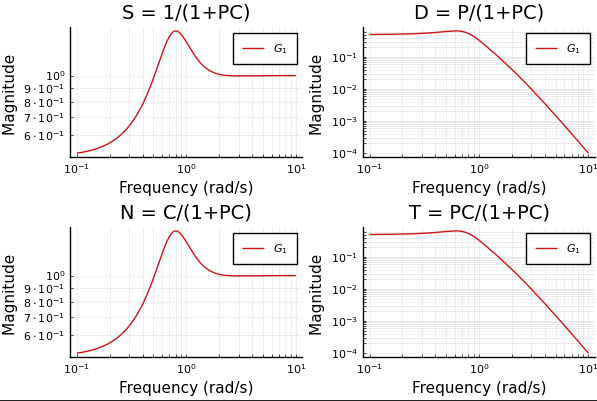
Ahora digamos que queremos un sistema de control con ancho de banda = 2 rad/s con cierto margen de fase dando un valor de rl:

ωp = 2 #Ancho de banda 
kp,ki,C2 = loopshapingPI(P,ωp,rl=1,phasemargin=60, doplot=true)
p1 = gangoffourplot(P, [tf(1), C2]); #Comparacion de los sistemas de control
p2 = nyquistplot([P, P*C2], ylims=(-2,2), xlims=(-3,3));
Plots.plot(p1,p2, layout=(2,1), size=(800,800)) #Formato para desplegar graficas